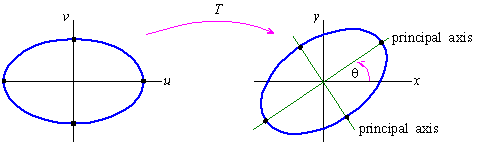
Rotation of Conics into Standard Form

If A, B, and  C are constants, then the level curves of
Q( x,y) = Ax2+Bxy+Cy2
(2)
are either lines, circles, ellipses, or hyperbolas.  If B ¹ 0, then a curve () is the image under rotation of a conic in standard position in the uv-plane.
 
Specifically, (2) is the image of a conic in standard position in the uv-plane of a rotation
é
ê
ë
x
y
 ù
ú
û 		= é
ê
ë
cos( q)
-sin( q)
sin( q)
cos( q)
ù
ú
û 		é
ê
ë
u
v
 ù
ú
û
(3)
that maps the u-axis to a principal axis of the conic, which is a line y = mx containing the points closest to or furthest from the origin.  

Thus, Lagrange multipliers can be used to determine the equation y = mx of a principal axis, after which replacing x and y by the rotation transformation implied by (1) and (3) will rotate a conic (2) into standard form.  

EXAMPLE 7    Rotate the following conic into standard form:
5x2-6xy+5y2 = 8
(4)

Solution: Our goal is to find the extrema of the square of the distance from a point ( x,y) to the origin, which is f(x,y) = x2+y2, subject to the constraint (4)  The associated Lagrangian is
L( x,y,l) = x2 + y2 - l(5x2 - 3xy + 5y2 - 21)
Since Lx = 2x-l( 10x-3y) and Ly = 2y-l(-3x+10y) , we must solve the equations
2x = l( 10x-6y) ,  2y = l( -6x+10y)
Since l cannot be zero since (0,0) cannot be a critical point, we eliminate l using the ratio of the two equations:
 2x
2y
   =    l( 10x-6y)
l(-6x+10y)
   or   x
y
   =    10x-6y
-6x+10y
Cross-multiplication yields 10xy-6x2 = 10xy-6y2 so that y2 = x2.  Thus, the principal axes - i.e., the lines containing the extrema - are  y = x and y = -x.  
       Using y = x means m = 1 and correspondingly,
é
ê
ë
x
y
 ù
ú
û 		= é
ê
ë
cos( q)
-sin( q)
sin( q)
cos( q)
ù
ú
û 		é
ê
ë
u
v
 ù
ú
û 		=  1
Ö2
 é
ê
ë
1
-1
1
1
 ù
ú
û 		é
ê
ë
u
v
 ù
ú
û
That is, x = ( u-v) /Ö2 and y = ( u+v) /Ö2, which upon substitution into (4) yields
5 æ
è 		 u-v
Ö2
 ö
ø 		2

 
 -6 æ
è 		 u-v
Ö2
 ö
ø 		æ
è 		 u+v
Ö2
 ö
ø 		+5 æ
è 		 u+v
Ö2
 ö
ø 		2

 
=
8
 5( u2-2uv+v2)
2
  -   6( u2-v2)
2
   +  5( u2+2uv+v2)
2
=
8
5u2 + 5v2 - 6u2 + 6v2 + 5u2 + 5v2
=
16
4u2 + 16v2
=
16
Consequently, the ellipse (4) is a rotation of the ellipse
u2  
4
    +   v2  
1
 = 16
as is shown below: