Rotations About the Origin   

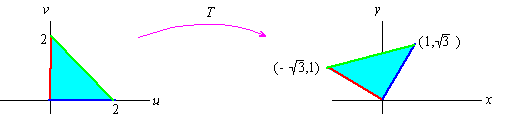
Rotations about the origin through an angle q are linear transformations of the form 

T( u,v) = á u cos( q) - v sin(q) ,u sin( q) + v cos( q) ñ

(1)

The matrix of the rotation through an angle q is given by

R( q) = é ê ë cos( q) -sin( q) sin( q) cos( q) ù ú û

when positive angles are those measured counterclockwise (see the exercises).           

EXAMPLE 5    Rotate the triangle with vertices ( 0,0), ( 2,0) , and ( 0,2) through an angle q = p/3 about the origin.       

Solution: To begin with, the matrix of the rotation is

R( q) = é ê ê ê ê ê ë cos æ è  p 3 ö ø -sin æ è  p 3 ö ø sin æ è  p 3 ö ø cos æ è  p 3 ö ø ù ú ú ú ú ú û = é ê ë 1/2 -Ö3/2 Ö3/2 1/2 ù ú û

so that the resulting linear transformation is given by

T æ ç è u v ö ÷ ø = é ê ë 1/2 -Ö3/2 Ö3/2 1/2 ù ú û é ê ë u v ù ú û

The point ( 0,0) is mapped to ( 0,0) . The point ( 2,0) is associated with [ 2,0] ^t, so that

T æ ç è 2 0 ö ÷ ø = é ê ë 1/2 -Ö3/2 Ö3/2 1/2 ù ú û é ê ë 2 0 ù ú û = é ê ë 1 Ö3 ù ú û

That is, ( 2,0) is mapped to ( 1,Ö3) . Similarly, it can be shown that ( 0,2) is mapped to ( -Ö3,1) :

       

cos(q) = 1  m2 + 1 sin(q) =  m  m2 + 1

é ê ë cos( q) -sin( q) sin( q) cos( q) ù ú û =  1  m2 + 1   é ê ë 1 -m m 1 ù ú û

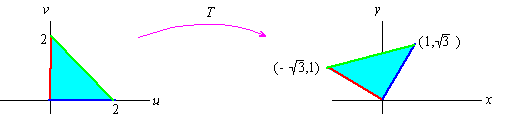
(1)

EXAMPLE 6    Rotate the triangle with vertices at ( 0,0) , (1,2) , and ( -4,2) so that one edge lies along the x-axis.

Solution: The line through ( 0,0) and (1,2) is y = 2x, which implies that the rotation matrix is

é ê ë cos( -q) -sin( -q) sin( -q) cos( -q) ù ú û =  1  22 + 1 é ê ë 1 2 -2 1 ù ú û

Thus, the point ( 1,2) is mapped to

T æ ç è 1 2 ö ÷ ø =  1 Ö5 é ê ë 1 2 -2 1 ù ú û é ê ë 1 2 ù ú û = é ê ë Ö5 0 ù ú û

while the point ( -1,4) is mapped to

T æ ç è -4 2 ö ÷ ø =  1 Ö5 é ê ë 1 2 -2 1 ù ú û é ê ë -4 2 ù ú û = é ê ë 0 2Ö5 ù ú û

Notice that this reveals that that the triangle is a right triangle.