Exercises:

Find the local extrema and saddle points of the following functions:

1. f( x,y) = x2+4y2 2. f( x,y) = x2-3y2 3. f( x,y) = x2+xy+3x+2y 4. f( x,y) = y2+xy-2x-2y 5. f( x,y) = x2-4xy+y2+6y 6. f( x,y) = -x2+2xy-y2+3x+4 7. f( x,y) = 3x2+6xy+7y2-2x+4y 8. f(x,y) = 4x2-6xy+5y2-20x+26y 9. f( x,y) = x3-3x2+y2 10. f( x,y) = x4+y4-y2 11. f( x,y) = x3+3xy+y3 12. f( x,y) = x3+6xy+y3 13. f( x,y) = 4xy-x4-y4 14. f( x,y) = x4+y4+4xy 15. f( x,y) = x4+2x2y-2y 16. f( x,y) = x4-2x2y+2y 17. f( x,y) = sin( x) +cos( y) 18. f( x,y) = xln( x) +yln( y) 19. f( x,y) = xsin( y) 20. f(x,y) = e2xcos( y)

Find the slope and y-intercept of the least squares line for each of the following data sets:

21. ( 1,1) , ( 2,2) , ( 3,3), (4,4) 22. ( 1,72) , ( 2,77) , (3,83), (4,97) 23. ( -1,1.2) , ( -2,2.3) , (-3,3.4) 24. ( 1,1) , ( 2,1) , ( 3,1) 25. ( 1,75) , ( 2,79) ,  ( 3,85),  ( 4,81) 26. ( 1,75) , (2,79) ,  ( 3,81) ,  ( 4,85)

27. Find the point in the plane z = x - y +1 which is closest to the origin. (Hint: minimize the square of the distance from a point ( x,y,x-y+1) to the origin ( 0,0,0) ).

28. Find the point in the plane z = x+2y+3 which is closest to the origin.

29. Find the point in the plane z = x+y closest to the point ( 2,2,1).

30. Find the point(s) on the surface z = ( x-1)²+y² closest to the origin.

31. What dimensions of a rectangular box with a surface area of 64 in² lead to a maximum volume?

32. What dimensions of a rectangular box with a volume of 64 in³ lead to a minimum surface area?

33. Acme sporting goods collected the following set of data relating price charged for a racket, x, to the number of rackets per week sold at that price. 

Fit this data to a linear demand function y = mx+b.

34. Repeat exercise 33 given the data set  

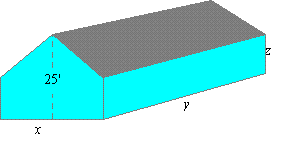
35.  A house with width x, length y, and height z is to have a roofline with a height of 25^¢.

If the house is to have a total floor space of 2000 ft², what values of x,y, and z minimize the sum of the area of the sides and the roof.

36. If the roof costs 3 times more than the sides of the house, then what values of x,y,z in problem 35 minimize the cost of the house?

37.  Suppose that r(t) = p+tu and L(s) = q + sw  where p, u, q, and w are constant vectors (i.e., r(t) and L(s) are straight lines).  Let E(s,t) denote the total squared distance between r(t) and L(s).  Does E(s,t) always have a minimum?  What is significant about any extrema or saddle points of E(s,t) when the two lines do not intersect?

LiveGraphics3d Applet

38. A "ray" travels in a line from the point ( 4,2) to the x-axis, is reflected in a straight line to the y-axis, and then is reflected again to the point ( 2,3) .

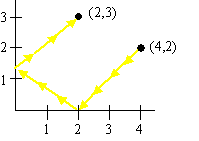
What is the shortest possible path for the ray to travel in this manner from ( 4,2) to ( 2,3) ?

39. Discussion: Explain why every point on the unit circle is a critical point of

f( x,y) = ( x2+y2-1) 2

Does f(x,y) have all saddle points on the unit circle, or does it have all minima on the unit circle? Explain.

40. Find the point(s) on the surface z = 1 - x² - y² closest to the origin. Why are there infinitely many of them?

41.   Write to Learn: Write a short essay in which you re-visit section 2 but instead assume that f_yy(p,q) is nonzero and subsequently complete the square in n. What does this version of the second derivative test look like?
42. *Write to Learn: The key to the proof of the second derivative test is equation (3), which is 

z"(0) = fxx( p,q) æ è m +   fxy( p,q) fxx( p,q) n ö ø 2    +   D( p,q) fxx( p,q)  n2

(3)

Although we say that there is "no information" when D(p,q) = 0, is that completely correct?  If f_xx(p,q) > 0 but D(p,q) = 0, then what does this imply about the possibility of an extremum at (p,q)?  How would we explore what happens for the one choice of m for which z"(0) = 0?  Is this one case enough to derail the entire theorem?  Write a short essay addressing these possibilities.

43.  *Suppose a house with a height of 10 feet at each corner is to have a total floor space of 2000 ft², and suppose that p_s is the cost per square foot of the sides and that p_r is the cost per square foot of the roof.

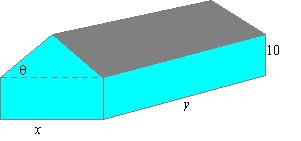
What width x, height y, and pitch of the roof q minimize the cost of the house? What shape should the house have if p_s £ p_r? What should the dimensions of the house be if p_s = 2p_r?