Exercises

Find the unit normal N and the curvature k( t) (using (5) ) of each of the following curves:

1. r( t) = á cos( 2t) ,sin( 2t) ñ 2. r( t) = á 3cos( pt) ,3sin( pt) ñ 3. r( t) = á 3t,4t+3 ñ 4. r( t) = á 5t+2,12t+3 ñ 5. r( t) = á 3sin( t) ,3cos( t) ,4t ñ 6. r( t) = á t3,3t2,6t ñ 7. r( t) = á t2,2t,ln( t) ñ 8. r( t) = á sin( t) ,cosh( t) ,cos( t) ñ 9. r( t) = á 3sin( t2),4sin( t2) ,5cos( t2) ñ 10. r( t) = á e2t,2et,t ñ

Find the linear acceleration dv/dt and the curvature k( t) ( using (7) ) of each of the following curves:

11. r( t) = á cos( 2t), sin( 2t) ñ 12. r( t) = á 3cos(pt),  3sin( pt) ñ 13. r( t) = á t, 2t3/2, 2( 1-t)3/2 ñ 14. r( t) = á2t, 3t, 4t+1 ñ 15. r( t) = á 2cos( t3/2), 2sin( t3/2), 2( 10-t)3/2 ñ 16. r( t) = á cos( t3/2), sin( t3/2), ( 4-t)3/2 ñ 17. r( t) = á 3t+4sin(t), 4t-3sin(t), 5cos(t) ñ 18. r( t) = á t + sin(t), t - sin(t), Ö2 cos(t) ñ 19. r( t) = á sin(t), cosh(t), cos(t) ñ 20. r( t) = á sin2(t), sin2(t), cos(2t) ñ 21. r( t) = á e2t, 2et, t ñ 22. r( t) = á t2, 2t, ln(t) ñ

Find the unit binormal and the torsion of each curve.  Is the curve restricted to a plane?

23. r( t) = á t, t, t2 ñ 24. r( t) = á 3sin( t) ,5cos( t) ,4sin(t) ñ 25. r( t) = á 3sin(t),  3cos(t),  4t ñ 26. r( t) = á 3sin( t2),3cos( t2) ,4t2 ñ 27.  r( t) = á 3sin(t), 5cos(t), 4sin(t) ñ 28. r( t) = á sin( t) ,cosh( t) ,cos( t) ñ

29. Find the equation of the line between the points P₁( 1,2,1) and P₂( 2,3,1) . Then find its linear acceleration dv/dt and its curvature. What is the curvature of a straight line and why?

30. Show that the graph of the vector-valued function

r( t) = á sec2( t) ,tan2( t) ñ

is a straight line. Then find its acceleration and its curvature.

31. Show that the graph of the vector-valued function

r( t) = á 4cos2( t) ,2sin( 2t) ñ

is a circle by showing that it has constant curvature. (Hint: 4cos²( 2t) -2 = 2( 2cos²( t) -1) )

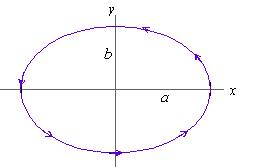
32. An ellipse with semi-major axis a and semi-minor axis b can be parameterized by

r( t) = á acos( t) ,bsin(t) ñ

for t in [ 0,2p] . Show that the curvature of the ellipse is

k( t) =   ab ( a2sin2 t + b2cos2 t ) 3/2

What is the curvature of the ellipse when a = b?

33. The function r( t) = á t,t³ ñ parametrizes the curve y = x³. Find the curvature of the curve and determine where it is equal to 0. What is significant about this point on the curve?

34.  Show that any curve with zero curvature must also have zero torsion.

35. Show that if r( t) = áx( t) ,y( t) ñ , then the curvature at time t is given by

k( t) =  | x' y'' - x'' y'| [ ( x' )2  +  ( y' )2  ]3/2

36. Use the fact that r( t) = á t,f( t) ñ parametrizes the curve y = f( x) to show that the curvature of the graph of a second differentiable function f( x) is

k(x) =   | f'' | [ 1 + (f' )2 ]3/2

37. Explain in your own words why at any point on a 3-dimensional smooth curve, the osculating circle must be in the plane with B as a normal.  

38. The curve r( t) = áRcos( t) ,Rsin( t) ñ is a circle centered at the origin. Compute the center of its osculating circle.  Is it what you expected?

39. Use the triple vector product to prove that 

T=N × B   and   N=B × T

and then use the result to show that

τ =   1 v  B  dN dt

40. The general form of a helix which spirals about the z-axis is given by

r( t) = á a cos(t),  a sin(t), bt ñ

where a > 0 and b > 0. Compute the curvature k and torsion t of the helix. How are they related to a and b.

41. In this problem, we consider the "compressed helix"

r( t) = á cos(t), sin(t), e-t ñ

1. What happens to the helix as t approaches ¥?
2. What value does k( t) approach as t approaches ¥?
3. What value does t( t) approach as t approaches ¥?

42. Suppose that r(t) is the position at time t of a planet as it orbits a sun located at the origin of a 3-dimensional coordinate system.

The angular velocity of the planet is L = r × v and the acceleration of the planet is 

a =   -GM r3  r

where M is the mass of the sun and G is the universal gravitational constant. Show that

v  × a =   GM r3  L

and then use this result to express the curvature of the planet's orbit as a function of r, v, G, M, and L. 

43. Show that if r( s) is parametrized by the arclength variable (that is, v = 1), then

v = T,    a = N,    B = v×a

and that

k =   dT ds          and       t =  dB ds ·N

44. Write to Learn: Write a short essay in which you show that a curve r( t) has zero torsion (i.e., t = 0 ) if and only if r( t) is a motion in a fixed plane.

45. Write to Learn: Write a short essay discussing the relationship between an automobile's odometer, speedometer, and accelerator. Does any instrument in an automobile measure the curvature of the automobile's path? Or are all the instruments and controls in an automobile related strictly to the linear components of acceleration?