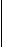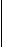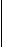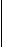Part 3: Curvature in the Plane

In order to better understand curvature, let's explore it for 2-dimensional curves.  If r( t) is the parametrization of a 2-dimensional curve, then its velocity can be written in polar form as

v = á vcos( q) ,vsin( q) ñ

Factoring out the v then leads to v = v  á cos(q) ,sin( q) ñ , which reveals that the unit vector is

T = á cos[ q( t) ], sin[ q( t) ] ñ

As a result, the derivative of T is given by

dT dt  =  d dt cos[ q(t) ],  d dt sin[ q( t) ]  =  -sin[ q( t) ] dq dt , cos[ q( t) ] dq dt  =  dq dt á -sin( q), cos(q) ñ

Since á -sin( q) ,cos( q) ñ is also a unit vector, the magnitude of dT/dt is

dT dt  =  dq dt

(9)

which via the chain rule is equivalent to

dT dt  =  dq ds ds dt

(10)

where s(t) is the arclength function of r(t) .  That is, the curvature of a 2-dimensional curve is given by

k = dq ds

or equivalently, moving a short distance ds along the curve causes a change dq in the direction of the velocity vector, where dq = kds.

Moreover, because of the relationship between curvature and the rate of change of q, we often use

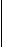k =  1 v  dq dt =  1 v  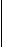dT dt

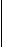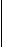to calculate the curvature (thus illustrating this important relationship).       

EXAMPLE 4    Find the curvature of the circle of radius 3 parametrized by

r( t) = á 3cos( t) ,3sin(t) ñ

Solution: Since the velocity is v( t) = á -3sin( t) ,3cos( t) ñ , the speed is

v =  9sin2( t) +9cos2( t)  = 3

As a result, the unit tangent vector is

T( t) = á -sin( t) ,cos(t) ñ

from which it follows that

dT dt  = á -cos( t) ,-sin(t) ñ

As a result, the curvature is

k =   1 v dT dt  =   1 3 cos2( t) +sin2( t)  =  1 3

As example 4 illustrates, curvature is closely related to the radius of a circle. Indeed, the osculating circle of a curve is the circle with radius

R = 1 k    or equivalently,   ds dq = R

and with a center at

Center = r + R N

Consequently, the osculating circle is practically the same as a small section of the curve, This allows us to interpret ds = Rdq mean that a short distance ds along the curve is practically the same as the small arc with angle dq on the osculating circle.

EXAMPLE 5    Find the curvature k of the curve r( t) = á ln| cos(t) |,  t ñ       

Solution: The velocity is

v =  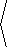1 cos(t)   d dt cos(t)  ,  1 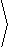= á -cos( t), 1 ñ 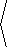-sin(t) cos(t)     ,  1

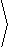which reduces to v = á -tan(t), 1 ñ.  Thus, the speed is

v = 1+tan2( t)  =  sec2( t) = sec( t)

and  the unit tangent vector is

T = 1  sec( t) á-tan(t), 1 ñ = á -sin(t),  cos(t) ñ

and the derivative of the unit tangent is

dT dt = á -cos( t), -sin(t) ñ

As a result, (5) implies that the curvature is

k =  1 v dT dt  =  1 sec(t) cos2( t)  + sin2( t)  =  cos(t)

It follows that R = 1/k and that

Center( t) = r( t)  +  R N( t) = á ln| cos(t)| ,t ñ +  1 cos( t) á -cos( t) ,-sin(t) ñ = á ln| cos(t)| -1,  t-tan( t) ñ

Indeed, the osculating circle itself at a fixed time t is given by

Osc( q) = Center( t)+R á cos( q) ,sin( q) ñ = á ln| cos(t) | - 1,  t - tan(t) ñ +  sec(t) á cos(q),sin(q) ñ

This is illustrated in the applet below:

If r(t) parameterizes a straight line, then its unit tangent is constant, and correspondingly, its curvature is k = 0. To illustrate, the curve r( t) = á ln| cos(t) |,  t ñ  in example 5 has a horizontal asymptote as t approaches p/2, and likewise, the curvature  k( t) = cos( t) a approaches 0 as t approaches p/2.  Since the relationship of the curvature and the radius of the osculating circle is

k = 1 radius of the osculating circle

the osculating circle becomes infinitely large as k approaches 0.       

Check your Reading: How is the curvature in example 4 related to the radius of the circle?