Multivariable Calculus Online

The Emphasis on Geometry

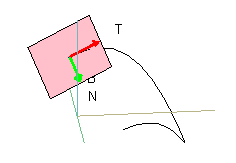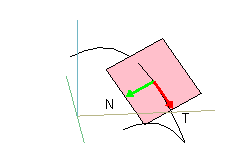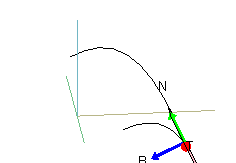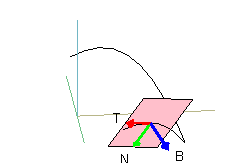
The difficulties that many students have with multivariable calculus frequently arise from their poor understanding of the concepts rather than their lack of computational skills.  Differentiation is not especially challenging in a multivariable setting, and techniques of integration are largely unnecessary.  Thus, it is the concepts in multivariable calculus—even generalizations of familiar topics such as limits and tangents—that often cause the most difficulty for students.

We discovered that as students began understanding the concepts in multivariable calculus, the course itself began to be too easy for them.  Students began to actively protest that the existing curriculum—i.e., the traditional sequence of topics—was unsubstantial and thus unrewarding in many aspects.  We began to be concerned that students might lose respect for the course as they recognized the lack of challenge in the material once they understood the definitions and ideas.  

Consequently, we felt justified in further transforming the multivariable course by placing greater and greater emphasis on geometry—indeed, in stopping just short of making the course an introduction to differential geometry itself.  We also felt justified in increasing the skill level of the course, such as in introducing the method of separation of variables for finding solutions to partial differential equations. 

We have been teaching this "higher level" version of the course for the past one and a half years, and it is this version of the course that is contained in the web site.  The course still enjoys a high rate of retention and success, and in fact, the course has become a highly enjoyable course for students and instructors alike.