Exterior Algebra and Exterior Calculus

The set of all differential forms has an elegant and important algebraic structure known as the Exterior Algebra for 3-dimensional space. Moreover, the calculus of differential forms is known as the Exterior Calculus and is also both important and elegant. Let's conclude by briefly describing differential forms using its more general structural properties.

To begin with, let us let W₀ denote the set of all functions U( x,y,z) that are infinitely differentiable with respect to each variable. We say that W₀ is the set of all 0-forms. Likewise, let us let W₁, W₂, and W₃ denote the set of all 1-forms, 2-forms, and 3-forms, respectively. In set notation, the set of all 1-forms is defined

W1 = { Mdx+Ndy+Pdz  |  M,N,P  are  in  W0}

the set of all 2-forms is defined

W2 = { Adx^dy+Bdx^dz+Cdy^dz   |  A,B,C  are  in  W0}

and 3-forms are given by W₃ = { d( x,y,z) dx^dy^dz  |  d  is  in  W₀} . We then define W = W₀ÈW₁ÈW₂ÈW₃ to be the set of all the differential forms.

On the set W, we have defined 2 important operations. To begin with, the wedge product between differential forms has the following properties.

If  w,a,b are in W and if k is a 0-form, then (i) (Distributive law) w^(ka+b) = kw^a+w^b (ii) (Antisymmetry) w^b = -b^w (iii) (nilpotence) w^w = 0

Secondly, for each k = 0,1,2, the d operator maps k-forms to k+1 forms. Moreover, it can be shown that d( dw) = 0.      

EXAMPLE 6    If w = xydx+yzdy+x³dz, find dw and show that d( dw) = 0.       

Solution: The definition of the differential operator leads to

dw = d( xy) ^dx + d( yz) ^dy + d( x3) ^dz = ( xdy+ydx) ^dx + ( zdy+ydz) ^dy + 3x2dx^dz = xdy^dx + ydx^dx + zdy^dy + ydz^dy + 3x2dx^dz = xdy^dx + ydz^dy + 3x2dx^dz

Since dw = xdy^dx+ydz^dy+3x²dx^dz, the quantity d( dw) yields

d( dw) = d( x) ^dy^dx + d( y) ^dz^dy + d( 3x2) ^dx^dz = -dx^dx^dy-dy^dy^dz + 6xdx^dx^dz = 0

The structure of differential forms is what implies all the results from the study of conservative fields. In particular, let us say that a differential form F in W is exact (or alternatively, conservative) if dF = 0.      

EXAMPLE 7    If F is a 2-form and S is a smooth solid with a simply-connected boundary, then what is the flux of dF through ¶S?       

Solution: Stoke's theorem for differential forms implies that

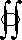¶S  dF = ó õ ó õ ó õ S  d( dF) = 0

since d( dF) = 0. Thus, the total flux of dF through the surface ¶S is 0.       

It can be shown that for ordinary 3-dimensional space, dF = 0 only if F = dU for some U in W, which is to say that a differential form F is exact only if it has a potential U. However, in more exotic spaces, a differential form may be exact without its having a potential, an idea which is growing in importance in science and engineering.