Reduction to Green's Theorem   

Stoke's theorem is a direct generalization of Green's theorem. Indeed, if we let F( x,y,z) = á M(x,y) ,N( x,y) ,0 ñ and suppose that S is in the xy-plane, then

Work = 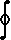¶S  F·dr = 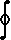¶S  á M,N ñ · á dx,dy ñ = 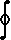¶S  Mdx+Ndy

Moreover, the curl formula in this case reduces to curl( F) = á 0,0,N_x-M_y ñ and the vector surface differential is dS = á 0,0,1 ñ dA since the unit surface normal to any region in the xy-plane must be the unit vector k = á 0,0,1 ñ .

LiveGraphics3d Applet

Thus, the flux of the curl of the vector field F through a region S in the plane is

flux = ó õ ó õ S curl( F) ·dS = ó õ ó õ S á 0,0,Nx-My ñ · á 0,0,1 ñ dA = ó õ ó õ S ( Nx-My) dA

Stoke's theorem is equivalent to ''flux of curl through S = Circulation over ¶S", which leads to

ó õ ó õ S ( Nx-My) dA = 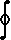¶S  Mdx+Ndy

That is, Stoke's theorem reduces to Green's theorem in the 2-dimensional xy-plane.      

EXAMPLE 2    Use Green's theorem to find the flux of F = á x, y+z, 2x ñ through the region S in the xy-plane enclosed by r( t) = át⁴-t²,t⁶-t² ñ , t in [ 0,1] .

LiveGraphics3d Applet

Solution: Since dS = kdA, the flux of F through S is

flux =   ó õ ó õ S á x,y+z,2x ñ · á0,0,1 ñ dA =   ó õ ó õ S 2xdA

If we apply Green's theorem with N_x = 2x and M_y = 0, then N = x² leads to

flux = 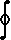¶S  0dx+x2dy

On the boundary curve, we have x = t⁴-t² and y = t⁶-t². Thus,

flux = ó õ 1 0  x2  dy dt dt = ó õ 0  ( t4-t2) 2( 6t5-2t) dt = ó õ 1 0  ( 6t13+4t9-12t11+4t7-2t5) dt = æ è  6t14 14 +  4t10 10 -  12t12 12 +  4t8 8 -  2t6 6 ö ø ê ê 1 0    =    -1 210

       

The xy-plane is not the only flat surface in 3-dimensional space. Other planes and surfaces yield different forms of Green's theorem. Let's look at an example.      

EXAMPLE 3    What does Stoke's theorem reduce to when S is a region in the yz-plane?

LiveGraphics3d Applet

Solution:  The vector i is the surface unit normal for the yz-plane, so dS = á 1,0,0 ñ dA_yz where dA_yz is the area differential for the yz-plane. Thus,

flux = ó õ ó õ S curl( F) ·dS = ó õ ó õ S áPy-Nz, Mz-Px, Nx-My ñ · á1,0,0 ñ dAyz = ó õ ó õ S ( Py-Nz) dAyz

Moreover, in the yz-plane, the displacement differential is dr = á 0,dy,dz ñ , so that the work integral reduces to

Work =  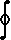 ¶S  F·dr = 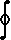¶S  á M,N,P ñ · á0, dy, dz ñ = 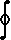¶S  Ndy + Pdz

Stoke's theorem says that ''flux through S = Work along ¶S", which in this case implies that

ó õ ó õ S ( Py-Nz) dAyz =  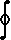¶S  Ndy+Pdz