Stoke's Theorem   

Our goal for the rest of this chapter is to generalize Green's theorem into several different contexts. Indeed, we will conclude with a very general statement of the fundamental theorem of calculus. We begin by generalizing Green's theorem to arbitrary surfaces, which is known as Stoke's theorem.

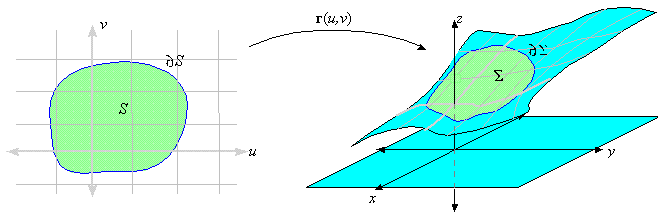
To begin with, suppose that F = á M,N,P ñ is a vector field through a surface r( u,v) = áx( u,v) ,y( u,v) ,z( u,v) ñ which maps a region S in the uv-plane to a surface S in R³. Also, let's assume that the boundary of S is mapped to the boundary of S. In addition, we require that ¶S has a counterclockwise orientation with respect to the unit surface normal n. This allows us to extend Green's theorem to the following:       

Stoke's Theorem: If F = á M,N,P ñ where M,N, and P are differentiable on a simply-connected region containing S, then

ó õ ó õ S curl( F) ·dS =  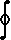¶S F·dr

That is, the flux of the curl of F through S is equal to the circulation of F around ¶S (recall that circulation is total work along a closed curve). A proof of Stoke's theorem is included at the end of this section.       

EXAMPLE 1    Find the flux of curl( F) through the paraboloid

r( u,v) = á ucos( v), usin( v) ,1-u2 ñ ,  u  in  [ 0,1] ,   v  in  [ 0,2p]

when F = á -y,x,z ñ , first by direct evaluation and then by Stoke's theorem.

LiveGraphics3d Applet

Solution: First, it is straightforward to show that curl( F) = á 0,0,2 ñ . Moreover, r_u = á cos( v) ,sin( v),-2u ñ and r_v = á -usin( v),ucos( v) ,0 ñ , so that

dS = ( ru×rv) du dv = á 2u2cosv,2u2sinv,u ñ du dv

Thus, the flux of the curl by direct evaluation yields

flux = ó õ ó õ S curl( F) ·dS = ó õ 1 0  ó õ 2p 0    á 0,0,2 ñ · á 2u2cosv,2u2sinv,u ñ dudv = ó õ 2p 0  ó õ 1 0  2ududv = 2p

        Alternatively, Stoke's theorem with F(x,y,z) = á -y,x,z ñ reduces to

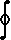ó õ ó õ S curl( F) · dS = ¶S  F·dr 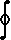= ¶S  á -y,x,z ñ · á dx,dy,dz ñ 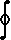= ¶S  -ydx+xdy+zdz

However, the boundary ¶S of the paraboloid is the unit circle (see above), which can be parameterized by r( t) = á cos( t) ,sin( t) ,0 ñ , t in [ 0,2p] . Thus, x = cos( t) , y = sin(t), and z = 0 yields

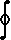ó õ ó õ S curl( F) · dS = unit circle   -ydx + xdy = ó õ 2p 0  æ è -y  dx dt +x  dy dt +0 ö ø dt = ó õ 2p 0  sin( t) sin( t) +cos(t) cos( t) dt = ó õ 2p 0  dt = 2p