Part 3: Line Integrals using the Arclength Parameter

Finally, recall that the speed of r( t) = á x( t) ,y( t) ,z( t) ñ , t in [ a,b] , is given by

ds dt  =  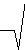   æ è dx dt ö ø 2    +  æ è dy dt ö ø 2    +  æ è dz dt ö ø 2

(5)

where ds is the arclength differential. As a result, if a line integral has the arclength differential ds, then

ó õ C  f( x,y) ds = ó õ b a  f( x,y)  ds dt  dt

where ds/dt is as given in (5).

EXAMPLE 5    Suppose that C is parameterized by r( t) = á 3cos(t), 3sin(t), 4t ñ for t in [ 0,2p] . Evaluate

ó õ C  x2ds

Solution: To do so, we notice that the velocity vector is

v( t) = á -3sin( t) ,3cos(t) ,4 ñ

so that the speed is

ds dt  =  9sin2( t) +9cos2( t) +16  = 5

Thus, the integral is

ó õ C  x2ds = ó õ 2p 0  x2  ds dt   dt = ó õ 2p 0  9cos2( t)   5  dt = 45 ó õ 2p 0  é ë  1 2 +  1 2 cos( 2t) ù û dt =  45p 2

       

Line integration with respect to arclength provides an alternative means of expressing the line integrals considered above. For example, if a smooth curve C is parameterized by r( t) , t in [ a,b] , then recall that

dr dt = T  ds dt

where T( t) is the unit tangent vector at time t and ds/dt is the speed. As a result, the work integral becomes

Work = ó õ C  F·dr = ó õ b a  F·  dr dt dt = ó õ b a  F·T  ds dt dt = ó õ C  F·T  ds

That is, the work integral also can be written in the form

Work = ó õ C  F·T  ds

(6)

EXAMPLE 6    Use (6) to find the work done by an object moving through a 2-dimensional vector field F(x,y) = á -y,x ñ along the circle C parameterized by

r( t) = á cos( t2) ,sin( t2) ñ ,  t  in   é ë 0, 2p ù û

   

Solution: The velocity of the curve is v( t) = á -2tsin( t²) ,2tcos( t²) ñ . It follows that the speed is ds/dt = 2t and the unit tangent vector is T = á -sin( t²) ,cos( t²) ñ . Thus, (6) becomes

Work = ó õ C  F·T  ds = ó õ Ö 2p F·T   ds dt dt 0

Since x = cos( t²) and y = sin( t²) , the vector field on the circle is F = á -y,x ñ = á -sin( t²) ,cos( t²) ñ , from which we obtain

Work = ó õ Ö 2p á -sin( t2) ,cos( t2) ñ · á -sin(t2) ,cos( t2) ñ   2tdt 0 = ó õ Ö 2p ( sin2( t2) +cos2( t2) )   2tdt 0 = ó õ Ö 2p   2tdt 0 = 2p