Triple Integrals in Spherical Coordinates

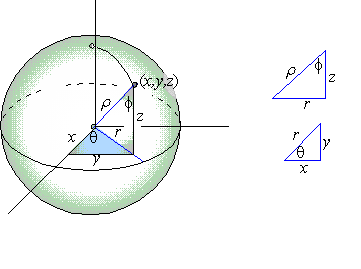
Suppose now that S is a solid bounded in spherical coordinates by q = a, q = b, f = p( q) , f = q( q) , r = f( f,q) , and r = g( f,q) , and recall that in spherical coordinates, the variables z and r are related to r and f by

r2+z2  =  r2 r  =  r sin(f) z  =  r cos(f)

That is, r,f are the ''polar'' coordinates for the zr-plane.  Since in the xy-plane, the differential is dy dx = r dr dq, so also in the zr-plane, the differential is

dz dr = r dr df

Thus, r dz dr dq becomes rr  drdf dq, so that (1) becomes

ó õ ó õ ó õ S  U( x,y,z) dV = ó õ b a  ó õ q( q) p( q)   ó õ g( f,q) f( f,q)   U( rcosq,rsin( q) ,rcos( f) )   rr  drdf dq

(2)

where r = rsin( f) . Although (2) is a quite useful tool for converting triple integrals into spherical coordinates, it is customary to use r = rsin( f) to eliminate r, thus producing the formula for change of variable into spherical coordinates

ó õ ó õ ó õ S  U( x,y,z) dV = ó õ b a  ó õ q( q) p( q)   ó õ g( f,q) f( f,q)   U( r,f,q)   r2sin( f)   drdfdq

where U( r,f,q) = U( r sin(f) cos(q),  r sin(f) sin(q),  rcos(f) ) .

In particular, remember that in spherical coordinates, the volume differential is given by either

dV = rr  dr df dq          or      dV = r2 sin(f)   dr df dq

Moreover, remember also the relationships given by the two right triangles relating ( x,y,z) to ( r,f,q) . (See the figure above).  In particular, x²+y² = r² implies x²+y² = r²sin²( f) and r²+z² = r² implies that

x2+y2+z2 = r2

(3)

Also remember that q ranges over [ 0,p] , while f ranges over [ 0,p] .

EXAMPLE 2    Use spherical coordinates to evaluate the triple integral

ó õ 1 -1  ó õ Ö 1-x2    -Ö 1-x2 ó õ Ö 1-x2-y2    -Ö 1-x2-y2 x2+y2+z2   dzdydx

Solution: To begin with, we notice that this iterated integral reduces to

ó õ ó õ ó õ   unit   sphere       x2+y2+z2   dV

As a result, in spherical coordinates it becomes

ó õ 2p 0  ó õ p 0  ó õ 1 0  r2   r2sin( f) dr df dq

since x²+y²+z² = r². Thus, we have

ó õ 2p 0  ó õ p 0  ó õ 1 0    r3  sin(f) dr df dq = ó õ 2p 0  ó õ p 0  ó õ 1 0    r3sin( f) dr df dq = ó õ 2p 0  ó õ p 0      r4 4 ê ê 1 0  sin( f)   dfdq =  1 4 ó õ 2p 0  ó õ p 0  sin( f)  dfdq =  1 4 ó õ 2p 0  -cos( f)  ê ê p 0  dq = p

       

EXAMPLE 3    Find the volume of the solid above the cone z² = x²+y² and below the plane z = 1.       

Solution: The cone z² = x²+y² corresponds to f = p/4 in spherical. Moreover, z = 1 corresponds to rcos( f) = 1, or r = sec( f) . Thus,

V = ó õ ó õ ó õ S  dV = ó õ 2p 0  ó õ p/4 0  ó õ sec( f) 0  r2sin( f) drdfdq = ó õ 2p 0  ó õ p/4 0   r3 3 ê ê sec( f) 0  sin( f) dfdq =  1 3 ó õ 2p 0  ó õ p/4 0  sec3( f)sin( f) dfdq

However, sec( f) sin( f) = tan(f) , so that

V =  1 3 ó õ 2p 0  ó õ p/4 0  tan( f) sec2( f) dfdq

Thus, u = tan( f) , du = sec²( f) df, u( 0) = tan( 0) = 0 and u( p/4) = tan( p/4) = 1 yields

V =  1 3 ó õ 2p 0  ó õ 1 0  ududq   =  1 3 ó õ 2p 0   1 2 dq =  p 3