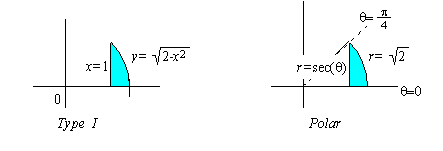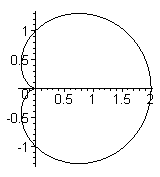Part 2: Areas and Volumes in Polar Coordinates

If R is a region in the xy-plane bounded by q = a, q = b, r = g( q) , r = f( q) , then (1) implies that

Area  of  R =  dA = ó õ b a  ó õ f( q) g( q)  rdrdq

thus allowing us to find areas in polar coordinates.       

EXAMPLE 2    Find the area of the region between x = 1, x = Ö2, y = 0, and

y = 2-x2

Solution: Since x = 1 corresponds to rcos( q) = 1 or r = sec( q) , the region is between the line r = sec( q) and a circle of radius Ö2 from q = 0 to q = p/4:

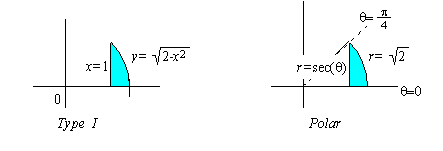
Thus, the area of the region is

Area =  dA = ó õ p/4 0  ó õ Ö2 sec( q)   rdrdq

and evaluation of the iterated integral leads to

Area = ó õ p/4 0   r2 2 ê ê Ö2 sec( q)   dq =  1 2 ó õ p/4 0  ( 2-sec2( q) ) dq =  1 2 ( 2q-tan( q) ) ê ê p/4 0 =  1 4 p-  1 2

Moreover, we can use polar coordinates to find areas of regions enclosed by graphs of polar functions.       

EXAMPLE 3    What is the area of the region enclosed by the cardioid r = 1+cos( q) , q in [ 0,2p] .

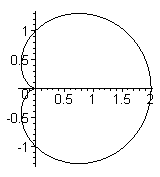
Solution: Since the cardioid contains the origin, the lower boundary is r = 0. Thus, its area is

Area = ó õ 2p 0  ó õ 1+cos( q) 0  rdrdq = ó õ 2p 0   r2 2 ê ê 1+cos( q) 0  dq

Substituting and expanding leads to

Area =  1 2 ó õ 2p 0  [ 1+2cos( q)+cos2( q) ]   dq =  1 2 ó õ 2p 0  é ë 1+2cos( q) +  1 2 +  1 2 cos( 2q) ù û dq =  1 2 æ è  3 2 q+2sin( q) +  1 4 sin( 2q) ö ø ê ê 2p 0  =  3p 2

       
Polar coordinates can also be used to compute volumes. For example, the equation of a sphere of radius R centered at the origin is

x2+y2+z2 = R2

Solving for z then yields shows us that the sphere can be considered the solid between the graphs of the two functions

g( x,y) = - R2-x2-y2 ,        f( x,y) =  R2-x2-y2

over the circle x²+y² = R² in the xy-plane.

Since circle x²+y² = R² defines the type I region

x = -R    y = -  R2-x2 x = R    y =   R2-x2

V = ó õ R -R  ó õ Ö R2-x2     2 R2-x2-y2   dydx -Ö R2-x2

(2)

EXAMPLE 4    Use polar coordinates to evaluate

V = ó õ R -R  ó õ Ö R2-x2     2 R2-x2-y2   dydx

Solution: To begin with, we rewrite the iterated integral as a double integral over the interior of the circle of radius R centered at the origin, which is often denoted by D:

V = óó õõ D      2 R2-x2-y2     dA

In polar coordinates, the disc D of radius R is bounded by the curves q = 0, q = 2p, r = 0, r = R, so that

V = óó õõ D      2 R2-x2-y2   dA = ó õ 2p 0  ó õ R 0  2 R2-x2-y2   rdrdq

Thus, if we let u = R²-r², then du = -2rdr, u( 0) = R², u( R) = 0, so that

V = - ó õ 2p 0  ó õ 0 R2  u1/2  du  dq = - ó õ 2p 0   u3/2 3/2 ê ê 0 R2  dq = ó õ 2p 0   2( R2) 3/2 3  dq =  4p 3 R3