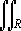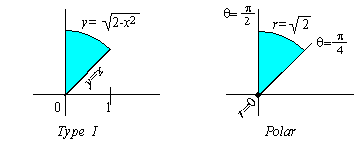Part 1:  Change of Variable into Polar Coordinates

We can also apply the change of variable formula to the polar coordinate transformation

To begin with, the Jacobian determinant is

¶( x,y) ¶( r,q) = ê ê ê cos( q) sin( q) -rsin( q) rcos( q) ê ê ê = rcos2( q) +rsin2( q) = r

As a result, the area differential for polar coordinates is

dA = ê ê  ¶( x,y) ¶( r,q) ê ê drdq = r dr dq

Let us consider now the polar region S defined by

q = a,q = b,r = g( q) ,r = f( q)

where f( q) and g( q) are contained in [ p,q] for all q in [ a,b] . If q₀,¼,q_m is an h-fine partition of [a,b] and r₀,¼,r_n is an h-fine partition of [ p,q] , then the image of [ a,b]×[ p,q] is a partition of the image of the region with near parallelograms whose areas are denoted by DA_jk:

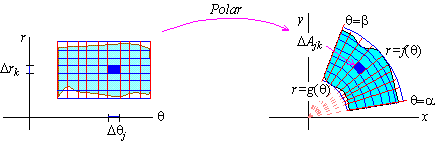
Since the area differential is dA = rdrdq, the area of the "near parallelogram" is approximately

Writing each of these limits as double integrals results in the formula for change of variable in polar coordinates:

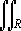f( x,y) dA = ó õ b a  ó õ f( q) g(q)   f( rcos(q), rsin(q) )   rdrdq

(1)

To aid in the use of (1), let us notice that if p is constant, then r = p is a circle of radius p centered at the origin in the xy-plane, while if a is constant, then q = a is a ray at angle a beginning at the origin of the xy-plane.

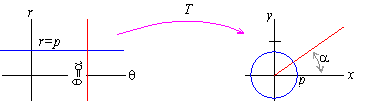
Polar coordinates for the origin are r = 0 for every value of q.       

EXAMPLE 1    Use (1) to evaluate

ó õ 1 0  ó õ Ö 2-x2 ( x2+y2) dydx x

Solution: To do so, we transform the iterated integral into a double integral

ó õ 1 0  ó õ Ö 2-x2 ( x2+y2)dydx =   ( x2+y2) dA x

where R is a sector of a circle with radius Ö2. In polar coordinates, R is the region between r = 0 and r = Ö2 for q in [ p/4,p/2] :

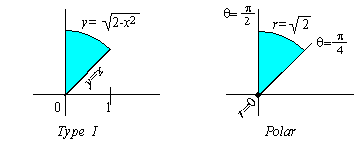
Since r² = x²+y², the double integral thus becomes

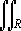( x2+y2) dA = ó õ p/2 p/4  ó õ Ö2 0  r2  rdrdq = ó õ p/2 p/4  ó õ Ö2 0  r3  drdq

and the resulting iterated integral is then easily evaluated:

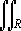( x2+y2) dA = ó õ p/2 p/4   r4 4 ê ê Ö2 0  dq = ó õ p/2 p/4  dq =  p 4