Exercises:

Evaluate the following iterated integrals by transforming to polar coordinates.

1. ó õ 1 0  ó õ Ö 1-x2 x2+y2 dydx 0 2. ó õ 1 0  ó õ Ö 1-x2 tan-1 æ è  y x ö ø dydx 0 3. ó õ 1 0  ó õ Ö 1-x2  x x2+y2  dydx 0 4. ó õ 1 0  ó õ Ö 1-x2  y x2+y2  dydx 0 5. ó õ 1 0  ó õ Ö 1-y2  y dxdy x2+y2 0 6. ó õ 1 0  ó õ Ö 1-y2  x dxdy x2+y2 0 7. ó õ 2 0  ó õ Ö 4-x2 9-x2-y2  dydx -Ö 4-x2 8. ó õ 2 -2  ó õ Ö 4-x2     x2-y2 x2+y2   dydx 0 9. ó õ 1 0  ó õ Ö 2-x2  x x2+y2   dydx x 10. ó õ 1 0  ó õ -Ö 2-x2  y x2+y2   dydx x 11. ó õ 1 0  ó õ x 0   x x2+y2   dydx 12. ó õ 1 0  ó õ x 0   x x2+y2   dydx 13. ó õ 1 0  ó õ Ö 2-y2  x x2+y2 dxdy 1 14. ó õ 1 0  ó õ Ö 2-y2  y x2+y2 dxdy 1 15. ó õ 1 0  ó õ Ö 1-x2  dydx [x2+y2] 3/2 1-x 16. ó õ 1 0  ó õ ¥ 1-y   dxdy [ x2+y2] 3/2

Each of the following polar curves encloses a region that contains the origin. Find the area of the region the curve encloses.

17. r = 5, q  in [ 0,2p] 18. r = 3, q  in [ -p,p] 19. r = sin(q) , q  in  [ 0,p] 20. r = 4cos(q) , q  in  [ 0,p] 21. r = pq - q2, q  in  [ 0,p] 22. r = | q | +1, q  in  [ -p,p] 23. r = sin(3q) , q  in  [ 0,2p/3] 24. r = 4cos(3q) , q  in  [ 0,2p/3] 25. r = sin(5q) , q  in  [ 0,2p/5] 26. r = sin2(q) , q  in  [ 0,p] 27. r = 1 + cos(2q) , q  in  [ 0,p] 28. r = 1 + sin( 3q) , q  in  [ 0,2p/3] 29. r = sin(q)  + cos(q) , q  in  [ 0,p] 30. r = 3sin(q) + 4cos( q) , q  in  [ 0,p]

31. Use polar coordinates to find the volume of a right circular cone with height h and a circular base with radius R

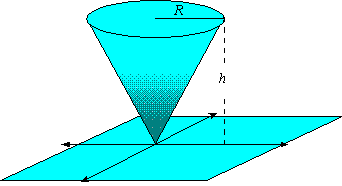
(hint: the equation of the cone is

z =  h R x2+y2

32. A right circular cone with a base of radius R is sliced by a plane of the form

z = h1 + ( h2 - h1)   x+R 2R

where h₁ and h₂ are positive. What is the shape of the solid between this plane and the xy-plane, and what is its volume?

33. Recall that if 0 < e < 1 and p > 0, then

r =  p 1-ecos( q)

is an ellipse which encloses a region R. Evaluate

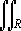dA [ x2+y2] 3/2

34. Evaluate the double integral

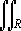ydA

where R is the polar ellipse described in exercise 33.

35. In example 5, what is the probability that

1. The final position of the ball is in the 1st quadrant and is no more than 5 feet from the origin.
2. The final position of the ball is between 3 and 7 feet from the origin.
3. The final position of the ball is in the unit square [0,1] × [0,1].

36.  After several throws at a dart board, a dart thrower finds that both the X and Y coordinates of his darts have a mean of 0 and a standard deviation of 3 inches. What is the probability that a randomly selected dart throw from all those he has thrown will be in the "bulls eye", if the bulls eye is a circle of radius one inch centered at the origin?

37. Suppose an airplane has two rocket engines that are expected to fire at a "time zero", and suppose that each engine's firing time is normally distributed with a standard deviation of s = 0.01 seconds. If the rockets' ignitions are independent events, what is the probability that the sum of the squares of the firing times is less than 0.01?

38.  In exercise 37, what is the probability that the left engine will fire no more than Ö3 times later than the right engine?

39.  The antennae lengths of a sample of 32 woodlice were measured and found to have a mean of 4 mm and standard deviation of 2.37 mm. Assuming the antennae lengths are normally distributed, what is the probability of one of the antennae of a woodlice being twice as long as the other? (Hint: substitute to translate the means to 0). 

40.  Acme sheet metal produces several hundred rectangular sheets of metal each day.  If errors in the lengths and widths of the rectangular sheets are independent random variables with mean of 0 and a standard deviation of s = 0.1 inches, then what is the probability that the error in the area of the rectangular sheets exceeds 0.1 inches?   

41. Use the method in the discussion preceding example 6 to evaluate

J = ó õ ¥ 0  x2e-x2dx

42. Find the area and the centroid of a cardioid of the form

r = 1+cos( q)

43. Write to Learn: A freezer produces ice cubes with normally distributed temperatures with a mean of 0^°F and a standard deviation of 2^°F. Write a short essay in which you estimate and explain the probability that two ice cubes chosen at random will have temperatures that differ by no more than 3^°F, assuming the temperatures of the cubes are independent.

44. Try it out! Drop a ball several times (i.e., 20-30 times) from a position directly above an ``origin'' in an xy-plane you create. (Hint: to avoid any bias, you might want to secure the ball with a thread and then release the ball by cutting the thread). Suppose that

( x1,y1) ,( x2,y2) ,¼,(xn,yn)

denotes the final stopping points of the ball. The sample means of both the x's and the y's should be practically zero. The sample standard deviation for the x's is

sx =       n å   j = 1  æ è   _ xj -   x ö ø 2 n - 1

and the sample standard deviation s_y for the y's is similar. Show that s_x » s_y and then repeat example 5 using the sample standard deviations as the value for s.