Part 4: Volumes of Solids over Type II Regions

Similarly, if p( y) £ q( y) for y in [ c,d] , then the region R in the xy-plane bounded by the curves x = p( y) and x = q( y) from  y = c  to y = d,

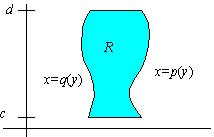
is said to be a type II region. Correspondingly, if f(x,y) ³ 0 for all ( x,y) in a type II region R, then the volume of the solid under z = f( x,y) and over the region R is
V = ó
õ 		d

c 
 ó
õ 		q( y)

p( y)  
 f( x,y)dxdy
(2)

       

EXAMPLE 6    Find the volume of the solid under the graph of f( x,y) = x2+y2 over the type II region
y in [0,1]
x = y2  to  x = y
Solution: To do so, we use (2) to see that
V = ó
õ 		1

0 
 ó
õ 		y

y2 
 ( x2+y2) dxdy
Evaluating the innermost integral leads to
V
=
ó
õ 		1

0 
 é
ë 		 x3
3
 +xy2 ê
ê 		y

y2 
 ù
û 		dy
=
ó
õ 		1

0 
 é
ë 		 4
3
 y3-  1
3
 y6-y4 ù
û 		dy
=
 3
35

       

Finally, let us note that unbounded regions can lead to convergent improper integrals. Indeed, unbounded solids can have a finite volume.       

 

EXAMPLE 7    Find the volume of the solid under the graph of f(x,y) = e-x-y over the first quadrant.

Solution: In the first quadrant, x is in ( 0,¥) and y is in ( 0,¥) . Thus, (2) implies that
V = ó
õ 		¥

0 
 ó
õ 		¥

0 
 e-x-ydydx
The inner integral is evaluated as an improper integral
V
=
ó
õ 		¥

0 
lim
R® ¥ 
 ó
õ 		R

0 
 e-x-ydydx
=
ó
õ 		¥

0 
lim
R® ¥ 
 (e-x-0-e-x-R) dx
=
ó
õ 		¥

0 
 e-xdx
The resulting integral is also evaluated as an improper integral, leading to
V =
lim
S® ¥ 
 ó
õ 		S

0 
 e-xdx =
lim
S® ¥ 
 ( e0-e-R) = 1