Chapter 3

Practice Test

Instructions.  

Show your work and/or explain your answers. (Note: Concepts from ''DIFF GEOM'' sections included only in the last problem).

 

1. Find the equation of the tangent plane to the level surface

   x+z2 = y+1

   at the point ( 2,2,1) . Solution: Since x-y+z² = 1, we let U( x,y,z) = x-y+z². Thus,

   ÑU =   á 1,-1,2z ñ

   The normal to the surface is n = á 1,-1,2 ñ and the equation is

   1( x-2) -1( y-2) +2( z-1) = 0

   which results in z = -x/2 + y/2 +1.
2. Find the level surface representation of the parametric surface

   r( u,v) = á vsin( u) ,v2,vcos( u) ñ

   Solution: Clearly, x = vsin( u) , y = v², and z = vcos( u) . We can eliminate u by noticing that

   x2+z2 = v2sin2( u) +v2cos2( u) = v2

   Since y = v², we eliminate v by noticing that x²+z² = y.
3. Find the level surface representation of the parametric surface

   r( u,v) = á eucosh( v),eusinh( v) ,e-u ñ

   Solution: Clearly, x = e^ucosh( v) , y = e^usinh( v) , and z = e^-u. To eliminate v we notice that

   x2-y2 = e2ucosh2( v) -e2usinh2( v) = e2u[ cosh2( v) -sinh2( v) ] = e2u

   To eliminate u, we notice that z² = e^-2u, so that

   ( x2-y2) z2 = e2ue-2u = 1

   so that the surface is given by x²z²-y²z² = 1.
4. Find the parametric equation of the tangent plane to the parametric surface

   r( u,v) = á vsin( u) ,v2,vcos( u) ñ

   at ( u,v) = ( p/4,1) . Solution: r_u = á vcos( u),0,-vsin( u) ñ and r_v = ásin( u) ,2v,cos( u) ñ . Thus, we have

   ru( p/4,1) =  1 Ö2 ,0,  -1 Ö2     and    rv( p/4,1) =  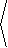1 Ö2 ,2,  1 Ö2

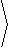   Since r( p/4,1) = á 1/Ö2,1,1/Ö2 ñ , the parameterization of the tangent plane is

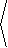
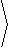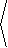
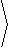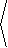
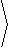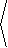
   L( du,dv) = r( p/4,1) +ru( p/4,1) du+rv( p/4,1) dv =  1 Ö2 ,1,  -1 Ö2 +  1 Ö2 ,0,  -1 Ö2 du+  1 Ö2 ,2,  1 Ö2 dv =  1 Ö2 +  du Ö2 +  dv Ö2 ,1+2dv,  -1 Ö2 -  du Ö2 +  dv Ö2

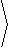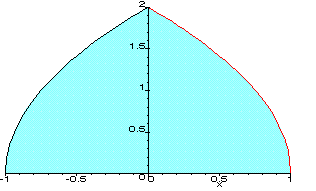
5. Find the image of the unit square under the coordinate transformation

   T( u,v) = á u2-v2,2uv ñ

   Solution: Since x = u²-v² and y = 2uv, we have

   v = 0:    x = u2,y = 0Þ x ³ 0 u = 1:    x = 1-v2,y = 2vÞ x = 1-  y2 4 v = 1:    x = u2-1,y = 2uÞ x =  y2 4 -1 u = 0:    x = -v2,  y = 0Þ x £ 0

   Putting them all together yields the following region:

 

6. Find the matrix of rotation through an angle of q = 45^°. Then use this to rotate the line v = u+1 through an angle of 45^°. Solution: The rotation matrix is

   Rp/4 = é ê ê ê ê ê ë cos æ è  p 4 ö ø -sin æ è  p 4 ö ø sin æ è  p 4 ö ø cos æ è  p 4 ö ø ù ú ú ú ú ú û = é ê ê ê ê ê ë  1 2 Ö2 -  1 2 Ö2  1 2 Ö2  1 2 Ö2 ù ú ú ú ú ú û

   Thus, rotation of the vector á u,v ñ results in

   T( u,v) = é ê ê ê ê ê ë  1 2 Ö2 -  1 2 Ö2  1 2 Ö2  1 2 Ö2 ù ú ú ú ú ú û é ê ë u v ù ú û = é ê ê ê ê ê ë  1 2 Ö2u-  1 2 Ö2v  1 2 Ö2u+  1 2 Ö2v ù ú ú ú ú ú û

   That is, x = Ö2u/2 - Ö2v/2 and y = Ö2u + Ö2v/2. Since v = u+1, we get

   x =  1 2 Ö2u-  1 2 Ö2( u+1) = -  Ö2 2 y = y =  1 2 Ö2u+  1 2 Ö2( u+1) = Ö2u+  1 2 Ö2

   Thus, v = u+1 is mapped to the line x = -Ö2/2.

 

7. Convert the following into polar coordinates and solve for r:

   y = 3x+1

   Solution: Since x = rcos( q) and y = rsin( q) , we have

   rsin( q) = 3rcos( q) +1,        r =  1 sinq-3cosq

 

8. Convert the following into polar coordinates and solve for r :

   x2+y2 = x+y

   Solution: r² = rcos( q) +rsin( q) implies that

   r = cos( q) +sin( q)

 

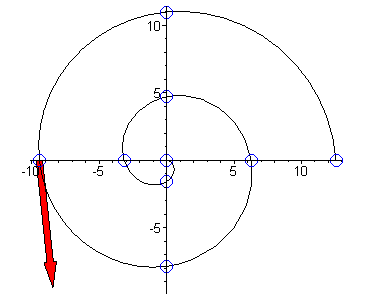
9. Sketch the graph of r = 4p-q in polar coordinates when q is in [ 0,4p] . Then find and sketch the tangent vector to the curve when q = p Solution: To sketch the curve, we use a table of values of r versus q :

   q 0  p 2 p  3p 2 2p  5p 2 3p  7p 2 4p r 4p » 12. 57  7p 2 » 11.0 3p » 9. 42  5p 2 » 7. 85 2p » 6. 28  3p 2 » 4. 71 p » 3.14  p 2 » 1. 57 0

   We plot the points in polar coordinates to obtain the curve. The Jacobian in polar coordinates yields the tangent vector:

   v = é ê ë cos( q) -rsin( q) sin( q) rcos( q) ù ú û é ê ë r' (q) 1 ù ú û

   Since r( p) = 3p and r' (q) = -1, we have

   v = é ê ë cos( p) -3psin( p) sin( p) 3pcos( p) ù ú û é ê ë -1 1 ù ú û = é ê ë 1 -3p ù ú û

   That is, the tangent vector is v = á 1,-3p ñ , which is shown in the plot above.

 

10. Find the Jacobian determinant and area differential of the coordinate transformation

    T( u,v) = á u-v,u2+v2 ñ

    Solution: Since x = u-v and y = u²+v², the Jacobian is

    ¶( x,y) ¶( u,v) =  ¶x ¶u  ¶y ¶v -  ¶x ¶v  ¶y ¶u = 1·2v-( -1) ·2u = 2u+2v

    Thus, the area differential is dA = | 2u+2v| dudv.

 

11. What is the unit surface normal for the surface x²+y²+z² = 2x? What is the unit surface normal for the surface in cylindrical coordinates? Solution: Writing x²+y²+z²-2x = 0 leads us to define U = x²+y²+z²-2x. Thus, ÑU = á2x-2,2y,2z ñ and

    || ÑU|| = ( 2x-2) 2+4y2+4z2   = 4x2-8x+4+4y2+4z2   = 4( x2-2x+y2+z2) +4   = 4( 0) +4   = 2

    Thus, the unit surface normal is

    n =  ÑU || ÑU|| = áx-1,y,z ñ

    (1)

    In cylindrical coordinates, U = r²+z²-2rcos( q) and the gradient is given by

    ÑU = Urer+  1 r Uqeq+Uzk

    where e_r = á cos( q) ,sin(q) ,0 ñ and e_q = á-sin( q) ,cos( q) ,0 ñ . Thus, in cylindrical coordinates, we have

    ÑU = ( 2r-2cos( q) ) á cos( q) ,sin( q) ,0 ñ +  1 r ( 2rsin( q) ) á -sin(q) ,cos( q) ,0 ñ +2z á0,0,1 ñ = á 2rcos( q) -2cos2( q) ,2rsin( q) -2cos( q) sin( q) ,0 ñ + á -2sin2( q) ,2sin( q) cos( q),0 ñ + á 0,0,2z ñ = á 2rcos( q) -2( cos2( q) +sin2( q) ) ,2rsin( q) -2cos( q) sin( q) +2cos( q) sin( q) ,2z ñ = á 2rcos( q) -2,2rsin( q),2z ñ

    That is, ÑU = á 2rcos( q) -2,2rsin( q) ,2z ñ , and as shown above, ||ÑU|| = 2, so that

    n =  ÑU || ÑU|| = á rcos( q) -1,rsin( q) ,z ñ

    Notice that you could have obtained the same result by simply applying cylindrical coordinates to (1).

 

12. Find the pullback of the surface x²+y²+z² = 2x into spherical coordinates, and then use the result to construct a parameterization of the surface. Solution: In spherical coordinates, r² = x²+y²+z² , r = rsin( f) and x = rcos( q) = rsin( f) cos( q) . Thus, the surface becomes

    r2 = rsin( f) cos( q)    or    r = sin( f) cos( q)    for  r ¹ 0

    Since also y = rsin( f) sin( q) and z = rcos( f) , the parameterization of the surface is

    r( f,q) = á rsin( f) cos( q) ,rsin( f) sin( q) ,rcos( f) ñ = á sin2( f) cos2( q),sin2( f) cos( q) sin( q) ,sin( f) cos( f) cos(q) ñ

 

13. Use the fundamental form of the plane in polar coordinates to find the length of the polar curve r = e^-q/4 , q in [0,2p] . Solution: The fundamental form of the plane in polar coordinates is given by

    ds2 = dr2+r2dq2

    which leads to an arclength formula of

    L = ó õ b a   ds dq   dq = ó õ 2p 0  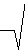r2+ æ è  dr dq ö ø 2       dq

    Substituting r = e^-q/4 and r^¢ = -e^-q/4/4 leads to

    
    

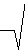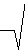
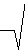
    L = ó õ 2p 0  e-q/2+  1 16 e-q/2     dq = ó õ 2p 0  e-q/4 1+  1 16     dq =  17 16         e-q/4 -1/4 ê ê 2p 0  = -e-p/2    Ö17  + Ö17

14. Find the fundamental form of the surface r( u,v) = á vsin( u) ,vcos( u) ,v ñ . Then use it to compute the arclength of

    v = sin æ è  u Ö2 ö ø ,    u    in     é ë 0,  p 4 ù û

    Solution: r_u = á vcos( u),-vsin( u) ,0 ñ and r_v = ásin( u) ,cos( u) ,1 ñ . Thus,

    g11 = ru·ru = v2cos2( u)+v2sin2( u) = v2 g12 = ru·rv = vcos( u) sin( u) -vsin( u) cos( u) = 0 g22 = rv·rv = sin2( u) +cos2( u) +1 = 2

    Thus, the fundamental form is

    ( ds) 2 = v2( du) 2+2( dv) 2

    and correspondingly, the arclength integral is

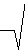
    L = ó õ p/4 0  v2+2 æ è  dv du ö ø 2       du

    Since dv/du = cos( u/Ö2) /Ö2, the arclength is

    
    

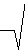
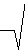
    L = ó õ p/4 0  sin2 æ è  u Ö2 ö ø +  2 ( Ö2) 2 cos2 æ è  u Ö2 ö ø       du = ó õ p/4 0  sin2 æ è  u Ö2 ö ø +cos2 æ è  u Ö2 ö ø     du = ó õ p/4 0  du =  p 4

 

15. DIFF GEOM: For the right circular cone, r( r,q) = á rcos( q) ,rsin( q) ,r ñ , do the following:
    1. Show that curves of the form q = k for k constant are geodesics on the cone. What are these curves?
    2. Find the fundamental form of the cone and calculate the shortest distance between the points with coordinates ( r,q) = ( 1,p) and ( r,q) = ( 3,p) .
    3. What are the principal curvatures of the surface?
    4. What are the mean and Gaussian curvatures of the surface? Do you obtain the same Gaussian curvature if you use the theorem Egregium?

Solution: (a) Curves of the form q = k are parameterized by

r( t) = á r( t) cos(k),  r( t) sin( k),  r( t) ñ

for some unknown function r( t) , and the acceleration is r'' ( t) = á r'' ( t) cos(k) ,  r'' ( t) sin( k) ,  r'' ( t) ñ . However, r_r = á cos(q) ,sin(q) ,1 ñ and r_q = á -rsin(q), rcos(q) ,0 ñ . Clearly, we have

r'' · rr = r'' cos2( k) +r'' sin2( k) +r''  = 2r''         and        r'' · rq = 0

If r'' = 0, then r(t) = pt + c for constants p and c. Thus, q = k constant and r = mt+b for m, b constant parameterizes a geodesic, which implies that q = k for k constant is a geodesic. These are straight lines on the cone that pass through the origin. 

(b) Since r_r = á cos( q) ,sin( q) ,1 ñ and r_q = á -rsin( q) ,rcos( q),0 ñ , we have g₁₁ = r_r·r_r = 2 and g₂₂ = r_q·r_q = r² with g₁₂ = 0 (the parameterization is orthogonal). Thus, the fundamental form is

ds2 = 2dr2+r2dq2

However, on q = k, the differential dq = 0, so that we have

ds = Ö2dr

Since r ranges from 1 to 3, this implies that

L = ó õ 3 1  Ö2dr = 2Ö2

(c) Since r_r×r_q = á -rcosq,-rsinq,r ñ , the surface normal is

n =  rr×rq || rr×rq|| =  1 Ö2 á-cos( q) ,-sin( q) ,1 ñ

Since r_rr = 0,  r_rq = á -sin(q), cos(q), 0 ñ and r_qq = á -r cos(q) , -r sin(q) ,0 ñ, the normal curvature of the cone is given by

kn( x) =  rrr·n || rr|| 2 cos2( x) +  rrq·n || rr||  || rq|| sin( 2x) +  rqq·n || rq|| 2 sin2( x) =   á -sin( q) ,cos( q) ,0 ñ · á -cos( q),-sin( q) ,1 ñ rÖ2 sin( 2x) +   á -rcos( q) ,-rsin(q) ,0 ñ · á -cos( q) ,-sin( q) ,1 ñ r2Ö2 sin2( x) =  r r2Ö2 sin2( x) =  1 rÖ2 sin2( x)

Thus, the principal curvatures occur when x = 0 and when x = p/2, and are correspondingly

k1 = 0        and        k2 =  1 rÖ2

(d) The mean curvature is

H = k1+k2 =  1 rÖ2

and the Gaussian curvature is 0 since k₁ = 0. Using the theorem Egregium, we obtain 

K =  -1 2Ög é ë  ¶ ¶q æ è  g11,q Ög ö ø +  ¶ ¶r æ è  g22,r Ög ö ø ù û

where g₁₁ = 2, g₂₂ =  r², and g = g₁₁g₂₂ = 2 r². Thus,   

K =  -1 2rÖ2 é ë  ¶ ¶q æ è  0 Ög ö ø +  ¶ ¶r æ è  2r rÖ2 ö ø ù û =  -1 2rÖ2 é ë  ¶ ¶q (0) +  ¶ ¶r æ è  2 Ö2 ö ø ù û = 0

Thus, the cone is a surface that can be ''made with a piece of paper'' without stretching or tearing the paper.