Principal Curvatures of a Surface

The identities 2cos2( q) = 1+cos(2q) and 2sin2( q) = 1-cos(2q) allow us to write the normal curvature as
kn( q)
=
L æ
è 		 1+cos( 2q)
2
 ö
ø 		+ Msin( 2q) + N æ
è 		 1-cos( 2q)
2
 ö
ø
=
æ
è 		 L-N
2
 ö
ø 		cos( 2q)  + Msin(2q)  +   L+N
2
As a result, kn( q) is a sine wave with period π with an amplitude of
Am = 
æ
è
L-N

2
ö
ø 		2

 
  + M2
and a mean value of ( L+N) /2
It follows that the maximum and minimum curvatures are given by k1 = ( L+N) /2+Am and k2 = ( L+N)/2-Am, respectively, which can be written as
k1 =  L+N
2
  + 
æ
è 		 L-N
2
 ö
ø 		2

 
 +M 2
 
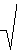    and    k2 =  L+N
2
  - 
æ
è 		 L-N
2
 ö
ø 		2

 
 +M 2
 
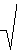(2)
The curvatures k1 and k2 are called the principal curvatures of the surface at the given point. Moreover, it is important to note that k1 and k2 always occur exactly p/2 radians apart.
       

EXAMPLE 2    What are the principal curvatures of the cylinder?       

Solution: Since kn( q) = -cos2(q) (see example 1), the largest possible curvature is k1 = -cos2( p/2) = 0 in the vertical direction, and the smallest possible curvature is k2 = -cos2( 0) = -1 in the horizontal direction.

       

The average of the principal curvatures is called the Mean curvature of the surface and is denoted by H. It can be shown that if C is a sufficiently smooth curve, then the surface with C as its boundary curve that has the smallest possible area must have a mean curvature of H = 0.  For example, consider two parallel circles in 3 dimensional space. 
LiveGraphics3d Applet

The catenoid is the surface connecting the two circles that has the least surface area, and a catenoid also has a mean curvature of H = 0. 
LiveGraphics3d Applet
 

Surfaces with a mean curvature of H = 0 are called minimal surfaces. For example, a soap film spanning a wire loop is a minimal surface.  Moreover, minimal surfaces have a large number of applications in architecture, mathematics, and engineering.  

       

EXAMPLE 3    Show that the Enneper Minimal Surface, which is parameterized by
r( u,v) =  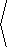 u-  1
3
 u3+uv2,    1
3
 v3-v-u2v, u2-v2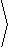
is in fact a minimal surface
LiveGraphics3d Applet
Solution: Since ru = á1-u2+v2,-2uv,2u ñ and rv = á2uv,v2-1-u2,-2v ñ , the second derivatives are
ruu = á -2u,-2v,2 ñ ,    ruv = á 2v,-2u,0 ñ ,    rvv = á2u,2v,-2 ñ
In addition, after a somewhat lengthy calculation, it can be shown that the unit surface normal is
n =  ru×rv
|| ru×rv||
=   á2u,2v,u2+v2-1 ñ
u2+v2+1
Moreover, || ru|| =  u2+v2+1, so that
L
=
 ruu·n
|| ru||2
 =   á -2u,-2v,2 ñ · á2u,2v,u2+v2-1 ñ
( u2+v2+1) 3
 =  -2( u2+v2+1)
( u2+v2+1) 3
 =  -2
( u2+v2+1) 2
M
=
 ruv·n
|| ru||  || rv||
=   á 2v,-2u,0 ñ· á 2u,2v,u2+v2-1 ñ
(u2+v2+1) 3
 = 0
N
=
 rvv·n
|| rv||2
 =   á 2u,2v,-2 ñ · á2u,2v,u2+v2-1 ñ
( u2+v2+1) 3
 =  2( u2+v2+1)
( u2+v2+1) 3
 =  2
( u2+v2+1) 2
Thus, the normal curvature is
kn( q) =  -2cos2( q)+2sin2( q)
( u2+v2+1) 2
The principal curvatures occur when cos( q) = 1, sin( q) = 0 and when sin( q) = 1, cos( q) = 0. Thus,
k1 =  -2
( u2+v2+1) 2
         and       k2 =  2
( u2+v2+1) 2
Since k1+k2 = 0, the mean curvature is H = 0 and the surface is a minimal surface.

       

 

Check your Reading: Is a cylinder a minimal surface?