In the first chapter, we developed a method for determining ' how much a curve is ``curving'' near a point. In this section, we extend the concept of curvature to a surface. In doing so, we will see that there are many ways to define curvature of a surface, but only one notion of curvature of a surface is intrinsic to the surface.

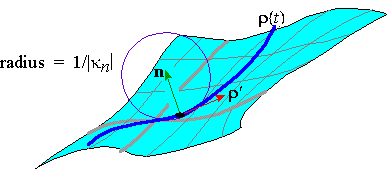
If r( t) is a geodesic of a surface, then r''  is normal to the surface, thus implying that r''  = kN where N = ± n. It follows that r'' · n = k  N · n = ±k, so that the curvature of the geodesic is given by k = ± r'' · n. As a result, we define the normal curvature k_n in the direction of r'  by

kn = r'' · n

Notice that k_n is positive if r'' and n point in the same direction, and is negative if r'' and n point in opposite directions.  The magnitude of k_n is the curvature of the geodesic formed by the normal section through r'.

Let's derive a formula for k_n when r( u,v) is an orthogonal parameterization of a surface and r( t) = r( u( t), v( t) ) is a geodesic on that surface. The chain rule implies that

r' ( t) = ru  du dt +rv  dv dt

It follows that the second derivative is

r''  =   dru dt  du dt +ru  d2u dt2 +  drv dt  dv dt +rv  d2v dt2

so that the normal curvature is given by

kn = r'' · n =    dru dt ·n  du dt +ru·n  d2u dt2 +  drv dt ·n  dv dt +rv·n  d2v dt2

However, r_u and r_v are orthogonal to n, so that

kn =  dru dt ·n  du dt +  drv dt ·n  dv dt = æ è ruu  du dt +ruv  dv dt ö ø ·n  du dt + æ è ruv  du dt +rvv  dv dt ö ø ·n  du dt = ruu·n æ è  du dt ö ø 2   +2ruv·n  du dt  dv dt +rvv·n æ è  dv dt ö ø 2

Finally, if we let du/dt = cos( q) || r_u|| ^-1 and dv/dt = cos( q) || r_v|| ^-1, then

r'  = cos( q)  ru || ru|| +sin( q)  rv || rv||

is a unit vector at an angle q to r_u. Substituting into k_n then leads to

kn =  ruu·n || ru|| 2 cos2( q) +2  ruv·n || ru||   || rv|| cos( q) sin( q) +  rvv·n || rv|| 2 sin2( q)

Thus, the normal curvature k_n( q) of the surface in the direction q measured from r_u is

kn( q) =  ruu·n || ru|| 2 cos2( q) +  ruv·n || ru||   || rv|| sin( 2q) +  rvv·n || rv|| 2 sin2(q)

(1)

We let L, M, and N denote the coefficients of cos²( q) , sin( 2q) , and sin²( q) , respectively.      

EXAMPLE 1    Let r( u,v) = á cos( u) ,sin( u) ,v ñ be a parametrization of the cylinder. Find the normal curvature k( q) of the cylinder.       

Solution: The partial derivatives of r( u,v) are

ru = á -sin( u) ,cos( u),0 ñ ,        rv = á 0,0,1 ñ ruu = á -cos( u) ,-sin( u),0 ñ ,    ruv = rvv = á0,0,0 ñ

Also, n = r_u×r_v = á cos(u) ,sin( u) ,0 ñ , so that r_uu·n = -cos²( u) -sin²( u) = -1 while r_uv·n = r_vv·n = 0. Finally, since | | r_u| | = || r_v| | = 1, the normal curvature is

kn( q) =  ruu·n || ru|| 2 cos2( q) +  ruv·n || ru||   || rv|| sin( 2q) +  rvv·n || rv|| 2 sin2(q) = -cos2( q) +0+0

That is, if we slice the cylinder along the vector v( q) through a normal to the surface at a point P, then the curvature at P of the curve formed by the intersection is k_n (q) = -cos²(q) .  To illustrate, consider that in the applet below each blue curve is a circle with radius 1/cos²(q).  

LiveGraphics3d Applet The angle is θ = thet °.      The curvature is κ n(θ) = -ax^2