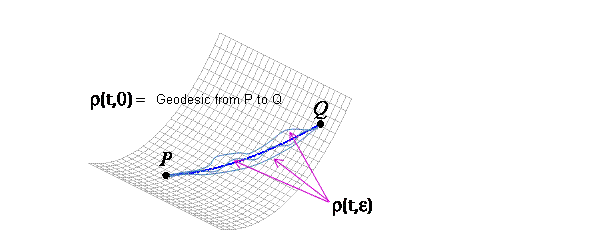
Geodesics

Intuitively, a geodesic between two points P and Q on a smooth surface r( u,v) is the "shortest" curve on the surface between the two points. To obtain a mathematical definition of a geodesic, let us suppose that for each e in some interval ( -c,c) , the curve r( t,e) = r( u( t,e) ,v( t,e) ) , t in [ a,b] , is a curve between P and Q and that

¶r ¶e ( a,0) =  ¶r ¶e ( b,0) = 0

(5)

Also, let us suppose that the shortest distance between P and Q exists and is along the curve r( t,0) = g( t) , where g(t) is a geodesic from P to Q with unit speed.

For each e in ( -c,c) , the length of r( t) is given by

L( e) = ó õ b a  Ö   r¢ · r¢   dt

Since a shortest distance occurs when e = 0, the length function L( e) must satisfy L' ( 0) = 0, which if we allow differentiation under the integral yields

L' ( e) = ó õ b a   ¶ ¶e Ö   r¢ · r¢   dt = ó õ b a   1 2 Ö r¢ · r¢  ¶ ¶e ( r¢ · r¢) dt = ó õ b a   1 2||r¢|| ( 2r¢ · re¢)  dt

Since ||r' (t, 0) || = ||g' (t) || = 1, at e = 0 we obtain

L¢( 0) = ó õ b a  g¢(t) · re¢( t,0) dt

(6)

The assumption (5) and integration by parts with u = g^¢( t) and dv = r_e^¢( t,0) dt, which implies that du = g^¢¢( t) and v = r_e(t,0) , results in

L¢( 0) = g¢(t)    ¶r ¶e (t,0) ê ê b a  - ó õ b a  g¢¢( t) ·  ¶r ¶e ( t,0) dt = - ó õ b a  g¢¢( t) ·  ¶r ¶e ( t,0) dt

Finally, the chain rule implies that

¶r ¶e = ru  ¶u ¶e +rv  ¶v ¶e

so that L^¢( 0) = 0 results in

ó õ b a  g¢¢· æ è ru  ¶u ¶e ( 0,t) +rv  ¶v ¶e ( 0,t) ö ø dt = 0 ó õ b a  ( g¢¢· ru)  ¶u ¶e (0,t) + (g¢¢· rv)  ¶v ¶e ( 0,t) dt = 0

Since u_e( 0,t) and v_e(0,t) are arbitrary, the integral is zero only when

g¢¢· ru = 0    and   g¢¢· rv = 0

That is, g''  is normal to the surface. This leads us to the following:    

Definition: If r( u,v) is the parameterization of a surface and if g( t) = r( u( t) ,v( t) ) for some functions u( t) and v( t) , then g( t) is a geodesic on r( u,v) if g^¢¢ is normal to the surface at every point on the curve, which is to say that

g'' · ru = 0    and   g'' · rv = 0

The concept of a geodesic is illustrated by the animation below:

EXAMPLE 5    Let r( u,v) = á cos( u) ,sin( u) ,v ñ be a parameterization of the right circular cylinder, and let g( t) = r( t,2t+1) be a curve on that surface. Show that g( t) is a geodesic on the cylinder.      

Solution: The expression r( t,2t+1) implies that u = t and v = 2t+1. Thus, g( t) = ácos( t) ,sin( t) ,2t+1 ñ , so that

g' ( t) = á -sin( t),cos( t) ,2 ñ         and        g''( t) = á -cos( t),-sin( t) ,0 ñ

Since r_u = á -sin( u) ,cos(u) ,0 ñ and r_v = á0,0,1 ñ and since u = t, we have

g'' · ru = cos( t)sin( u) -cos( u) sin( t) = cos( t) sin( t) -cos( t) sin( t) = 0

Likewise, g'' ·  r_v = 0·cos( t) -0·sin( t) +2·0 = 0. Thus, g( t) = r( t, 2t+1) is a geodesic on the cylinder.

LiveGraphics3d Applet

In general, the geodesics on the plane are straight lines, and the geodesics on the right circular cylinder parameterized by

r( u,v) = á cos( u) ,sin(u) ,v ñ

are the images of the straight lines after the plane has been rolled up into a cylinder-i.e., circles, vertical lines, and helices that are curves of the form

g( t) = r( at+b,ct+d)

where a, b, c, and d are constants.

In general, if a surface r( u,v) contains a straight line L( t) = mt+b, then L^¢( t) = m and L^¢¢( t) = 0. Thus, L^¢¢· r_u = 0 and L^¢¢· r_v = 0, which implies that any straight line contained within a surface must be a geodesic of the surface.        

EXAMPLE 6    Show that the catenoid x²+y²-z² = 1 can be parameterized by

r( u,v) = á cos(v)-usin( v),sin( v) +ucos( v) ,u ñ ,  u in ( -¥,¥) ,  v in [ 0,2p]

and then show that g( t) = r(t,q) is a straight line for each fixed value of q in [ 0,2p] . Solution: Since x = cos( v) -usin( v) and y = sin( v) +ucos( v) , we have

x2+y2 = ( cos( v) -usin( v) )2+( sin( v) +ucos( v) ) 2 = cos2( v) -2ucos( v) sin( v)+u2sin2( v) +sin2( v) +2ucos( v) sin( v)+u2cos2( v) = cos2( v) +sin2( v) +u2( cos2( v) +sin2( v) ) = 1+u2

Thus, x²+y²-z² = 1 since z = u. The curve

g( t) = á cos(q)-tsin(q) ,sin( q) +tcos( q),t ñ

has a derivative of g^¢( t) = á -sin( q) ,cos( q),1 ñ , so that g^¢¢(t) = 0 (differentiation is in the variable t) and g( t) must be a straight line. The lines are geodesics of the catenoid and are shown in the figure below:

LiveGraphics3d Applet

In addition, if r'' is normal to the surface, then the tangential acceleration of r( t) is zero and consequently, a geodesic r( t) has constant speed.