Tangents and Normals to Graphs of Functions

If f( x,y) is differentiable at ( p,q) , then linearization of f( x,y) at ( p,q) leads to a tangent plane to z = f( x,y) at ( p,q,f( p,q)) of

z = f( p,q) +fx( p,q) ( x-p) +fy(p,q) ( y-q)

This formula was developed using the total derivative.

However, we can also find the tangent plane to z = f( x,y) at ( p,q,f(p,q) ) by (a) considering the level surface z-f(x,y) = 0 or (b) considering the parameterization r( u,v) = á u,v,f( u,v) ñ at the point r( p,q) . The result is the same for all 3 methods.    

EXAMPLE 5    Find the equation of the tangent plane to f(x,y) = x² - y² at ( 1,2) by (a) linearization of f( x,y) at (1,2)  (b) considering the surface z-   f( x,y) = 0 at ( 1, 2,  f(1,2) ) and (c) finding the tangent plane to a parameterization of the form

r( u,v) = á u, v, f(u,v) ñ

at r( 1,2) .  The answer should be the same in all 3 cases.    

Solution:  (a) Since f_x = 2x and f_y = -2y, we have f_x( 1,2) = 2, and f_y( 1,2) = -4. Thus, f(1,2) = -3 and correspondingly, the equation of the tangent plane is

z = f( p,q) +fx( p,q) ( x-p)+fy( p,q) ( y-q) = -3+2( x-1) -4( y-2)

which simplifies to z = 2x-4y+3.  (b) If U( x,y,z) = z - (x²-y²) , then

ÑU = á -2x, 2y, 1 ñ

Since f(1, 2) = -3, the point of tangency is (1, 2, -3) and

ÑU( 1,2,-3 ) = á -2,4,1 ñ

Using ÑU( 1,2-3) as the normal, we obtain

-2( x - 1) + 4( y - 2) + 1( z - 3) = 0

which upon solving for z yields z = 2x - 4y + 3.  (c)  If we let

r( u,v) = á u, v, u2 - v2 ñ

then r_u = á 1,0,2u ñ and r_v = á 0,1,-2v ñ . Thus,

ru( 1,2) = á 1, 0, 2 ñ     and    rv( 1,2) = á 0, 1, -4 ñ

and r_u( 1,2) × r_v( 1,2) = á -2,4,1 ñ , which is the same as ÑU(1,2,-3) . Since r( 1,2) = á1, 2, -3 ñ , the equation of the tangent plane is again

z = 2x-4y+3

LiveGraphics3d Applet

 

Of course, in applications only one approach is necessary.  But there are applications when one method is preferred over another. For example, there are applications when it is necessary to have an orthonormal basis for the tangent plane -- i.e., two unit vectors e_u and e_v in the plane that are perpendicular to each other. For an orthogonal parameterization r(u,v), we need only rescale r_u and r_v into unit vectors e_u and e_v, respectively, to obtain the desired orthonormal basis (such rescaling is known as normalization).

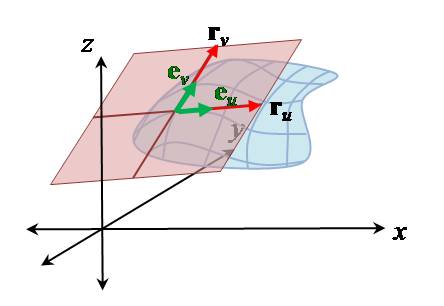
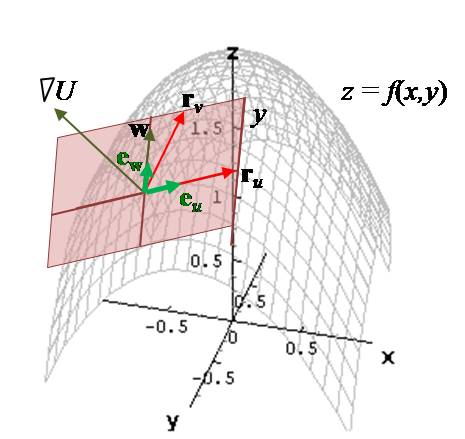
However, if r( u,v) = á u, v, f(u,v) ñ, then r_u ^.  r_v = f_uf_v , which is typically non-zero.  However, if we let U(x, y, z) = z - f(x,y) where x = u, y = v, then the vector

w = ÑU × ru

is in the tangent plane and is perpendicular to  r_u .  Normalizing  r_u and w results in an orthonormal basis for the plane.

Conversely, proofs of theorems often begin with an assumption that a parametric or level surface implicitly defines z as a function z = f(x,y) in a coordinate patch of the surface containing a given point, thus allowing techniques and ideas as in chapter 2 (or we may assume that x is implicitly defined as a function of y, z, etcetera).