The Inverse Function Theorem

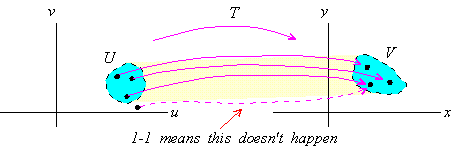
Recall that if a coordinate transformation T maps an open region U in the uv-plane to an open region V in the xy-plane, then T is 1-1 if each point in V is the image of only one point in U.
Additionally, if every point in V  is the image under T(u,v) of at least one point in U, then T(u,v) is said to map U onto V.

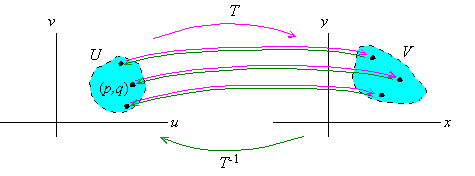
If T( u,v) is a 1-1 mapping of a region U in the uv-plane onto a region V in the xy-plane, then we define the inverse transformation of T from V onto U by
T-1( x,y) = ( u,v)   only  if  (x,y) = T( u,v)
The Jacobian determinant can be used to determine if T has an inverse transformation T-1 on at least some small region about a given point.       
Inverse Function Theorem: Let T( u,v) be a coordinate transformation on an open region S in the uv-plane and let (p,q) be a point in S. If
 ( x,y)
( u,v)
ê
ê

( u,v) = ( p,q)  
  ¹ 0
then there is an open region U containing ( p,q) and an open region V containing ( x,y) = T( p,q) such that T-1 exists and maps V onto U.

The proof of the inverse function theorem follows from the fact that the Jacobian matrix of T-1(x,y), if it exists, is given by the inverse of the Jacobian of T,
  J-1( x,y)  =    ( x,y)
( u,v)  		-1
 

 é
ê
ë 		 
yv
-xv
-yu
xu
 ù
ú
û 		   
which features a Jacobian determinant with a negative power (see the exercises). Thus, J-1 exists only if the determinant of J(u,v) is non-zero.        

EXAMPLE 7    Where is T( r,q) = á r cos(q), r sin(q) ñ invertible?   

Solution: The Jacobian determinant for polar coordinates is
 ( x,y)
( r,q)
 = r
which is non-zero everywhere except the origin. Thus, at any point (r0,q0) with r0 > 0, there is an open region U in the rq-plane and an open region V containing ( x,y) = ( r0cos( q0) ,r0sin( q0) ) such that T-1( x,y) exists and maps V onto U.

We will explore the result in example 7 more fully in the exercises. In particular, we will show that
T-1( x,y) =
x2+y2
, 2tan-1 æ
ç
è 		 y
x+
x2+y2

ö
÷
ø

Clearly, T-1 is not defined on any open region containing (0,0) . Also, if y = 0 and x > 0, then
2tan-1 æ
ç
è 		 y
x+
x2+02

ö
÷
ø 		  = 2tan-1 æ
è 		 0
x+ |x|
ö
ø 		= 0
But if y = 0 and x < 0, then
2tan-1 æ
ç
è 		 y
x+
x2+y2

ö
÷
ø 		   = 2tan-1 æ
è 		 0
x+| x|
ö
ø 		= 2tan-1 æ
è 		0
0
 ö
ø
That is, a different representation of T-1 must be used on any region which intersects the negative real axis.