Constrained Optimization

For example, let's suppose that g(x,y) = k is a closed curve with a parameterization of the form r(t) = á x(t), y(t) ñ for t in [a,b].  Finding the extrema of f(x,y) subject to g( x,y) = k is equivalent to finding the absolute extrema of the function z(t) = f(x(t), y(t)) for t in [a,b].  

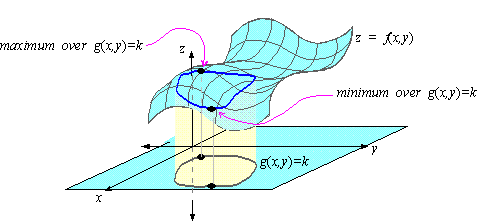
Because the curve is closed and z(a) = z(b), the extrema must occur at the critical points of z(t) = f( x(t), y(t) ).  However, the critical points occur when 

dz dt = Ñf · v = 0

where v is the velocity of r(t) . That is, the critical points of  z(t) occur when Ñf ^ v.  Since also Ñg ^ v, it follows that the extrema of f( x,y) subject to g( x,y) = k occur when Ñf is parallel to Ñg.

Let's view this in a different way.  As the levels of f( x,y) increase, short sections of level curves of f( x,y) form secant curves to g(x,y) = k

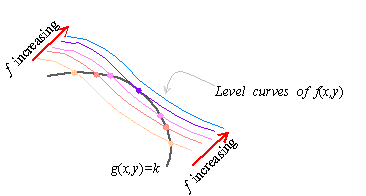
It follows that the highest level curve of f(x,y) intersecting g(x,y) = k must be tangent to the curve g(x,y) = k, which is possible only if their gradients Ñf and Ñg are parallel.

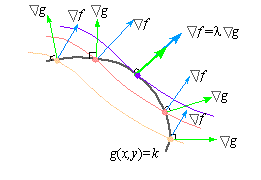
If Ñf is parallel to Ñg, then there is a number l for which

Ñf = lÑg

Thus, the extrema of f(x,y) subject to g( x,y) = k must occur at the points which are the solution to the system of equations  

á fx, fy ñ = lá gx, gy ñ,        g( x,y) = k

(1)

We call (1) a Lagrange multiplier problem and we call l a Lagrange multiplier.  

A good approach to solving a Lagrange multiplier problem is to first eliminate the Lagrange Multipler  l  using the two equations f_x = lg_x and f_y = lg_y .  The result along with the constraint g(x,y) = k can then be solved for x and y, and thus, the critical points.  Finally, since the constraint g(x,y) = k is a closed curve, the extrema of  f(x,y) over g(x,y) = k are the largest and smallest values of f(x,y) evaluated at the critical points.

EXAMPLE 1    Find the extrema of f( x,y) = xy+14 subject to

x2+y2 = 18

Solution: That is, we want to find the highest and lowest points on the surface z = xy+14 over the circle x² + y² = 18:

LiveGraphics3d Applet

If we let g( x,y) = x² + y², then the constraint is g(x,y) = 18. The gradients of f and g are respectively

Ñf = á y, x ñ         and        Ñg = á 2x, 2y ñ

As a result, Ñf = lÑg implies that y = l2x and x = l2y. Clearly, x = 0 only if y = 0, but (0,0) is not on the circle. Thus, x ¹ 0 and y ¹ 0, so that solving for l yields

l =  y 2x     and     l =  x 2y         Þ          y 2x =  x 2y

Cross-multiplying then yields 2y² = 2x², which is the same as y² = x². Thus, the constraint x²+y² = 18 becomes

x2+x2 = 18,        x2 = 9,        x = ±3

Moreover, y² = x² implies that either y = x or y = -x, so that the solutions to (1) are

( 3,3) ,  ( -3,3) ,  ( 3,-3) ,  (-3,-3)

However, f( 3,3) = f( -3,-3) = 23, while f(-3,3) = f( 3,-3) = 5. Thus, the maxima of f(x,y) = xy+14 over x²+y² = 18 occur at ( 3,3) and ( -3,-3) , while the minima of f( x,y) = xy+14 occur at ( -3,3) and ( 3,-3) .

LiveGraphics3d Applet