Exercises:

Let v( t)  and a( t)  denote the velocity and acceleration, respectively, of a vector-valued function r( t) .  Also, let r = ||r|| , v = ||v|| , and a = ||a|| ; let

r2 = r·r,  v2 = v·v,    and    a2 = a·a;

and let m, k, c, and L be constant.  Use theorem 7.1 to evaluate the following. Then expand and find the derivative directly. Show that both approaches produce the same result.

1. r' (t)  if r( t) = et u( t)    and   u( t) = á cos(t), sin(t) ñ 2. r' (t)  if r(t) = et u( t)    and   u( t) = á sin(2t), sin(t) ,cos(t) ñ 3. r' (t)  if r( t) = á t2, 2, 1 ñ × át3, 1, 2 ñ 4. r' (t)  if   r( t) = á t2,  et, 2t ñ × k 5.  dr dt    if r(t) = á cos(t) ,sin( t) ,t ñ  (note:   dr dt  =  d dt   ( r·r) 1/2 ) 6.  dr dt    if r(t) = át, t, t ñ (note:   dr dt  =  d dt   ( r·r) 1/2 )

Find the speed and unit tangent vector for each r(t) .

7. r( t) = á 3t,4t+3 ñ 8. r( t) = á 5t+2,12t+3 ñ 9. r( t) = á t2,2t,ln( t) ñ 10. r( t) = át3,3t2,6t ñ 11. r( t) = á 3sin( t2),4sin( t2) ,5cos( t2) ñ 12. r( t) = á sin( t) ,cosh( t) ,cos( t) ñ 13. r( t) = á e2t,2et,t ñ 14. r( t) = á sin( t),cos( t) ,ln| sec( t) | ñ

Find the arclength of the given curve over the given interval.

15. r( t) = á cos(2t), sin(2t) ñ 16. r( t) = á 3cos(pt),  3sin( pt) ñ t in [ 0,p] t in [ 0,1] 17. r( t) = á 2cos2(q), 2sin(q) cos(q) ñ 18. r( t) =  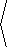cos( q) cos( q) +sin( q) ,  sin( q) cos( q)+sin( q)  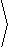 q in [ 0,p] q in æ è 0,  p 2 ö ø 19. r( t) = á cos(3t), sin(3t), 4t ñ 20. r( t) = á cos(t), sin(t), t ñ t in [ 0,p] t in [ 0,p] 21. r( t) = á 3t, 4t, 5cosh( t) ñ 22. r( t) = á cos(t), cosh(t), sin(t) ñ t in [ 0,ln( 2) ] t in [0,ln( 2) ] 23. r( t) = á cos(t), sin(t), 2t3/2 ñ 24. r(t) =  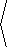sin( t) cosh( t) ,  cos( t) cosh( t) ,  sinh(t) cosh( t)   t in ( 0,1) t in [ 0,p]

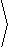Find the arclength function for the given curve.

25. r( t) = á sin( t3), cos( t3) ñ 26. r(t) = á t, t3/2 ñ 27. r( t) = á sin(t), cosh(t), cos(t) ñ 28. r( t) = á 3 sin(t2),  4 sin(t2),  5 cos(t2) ñ 29. r( t) = á t2, 2t3, 2( 1 − t2)3/2 ñ 30. r( t) = á sin(t), cos(t), ln| sec( t) | ñ 31. r( t) = á e2t,2et,t ñ 32. r( t) = á 3t, 4t, 5( 1 − t2)1/2  ñ

33. Find the arclength function and the arclength parameterization of the circle

r( t) = á cos( ln t) ,sin( ln t) ñ ,  t > 0

34. Find the arclength function and the arclength parameterization of the helix

r( t) = á 3cos( t) ,3sin(t) ,4t ñ

35. If a wheel of radius 0.25 is rolled around the inside of the unit circle,

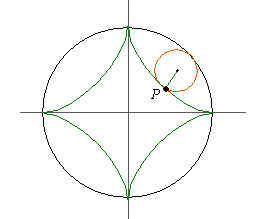
then the point P which is initially at ( 1,0) traces out a curve known as an astroid. Plot the parameterization of the astroid, which is

r( t) = á cos3( t) ,sin3( t) ñ ,    t  in  [ 0,2p]

Then find the arclength of this astroid curve.

36. The line y = mx+b is parameterized by r( t) = át, mt+b ñ . What is the arclength parameterization of the line?

37. Show that if q is the angle implied by an arc of length s on a circle of radius R,

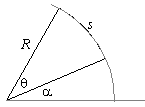
then s = Rq. (Hint: use the parameterization r( t) = á Rcos(t), Rsin( t) ñ for t in [ a,a+q] .

38. Show that if r( t) has constant speed v, then its arclength parameterization is

r s v

39. Suppose that r( t) satisfies the harmonic oscillator equation, which is 

ma = -w2r

where m and w are constant and a = r''.  Show that if

h =  1 2 mv2+  1 2 w2r2

then h is constant (hint: what is h' ( t) )?

40. Suppose that r( t) satisfies the inverse square law of attraction, which is 

a =  -k r3 r

where k is constant and a = r''.  Show that if

h =  1 2 v2-  k r

then h is constant (hint: what is h' ( t) )?

41. The Cayley transform (i.e., stereographic projection of the circle) is the mapping of the real line into the unit circle given by

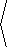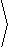
r( t) =   t2-1 t2+1  ,   2t t2+1

1. Derive the parameterization by using similar triangles to associate t with x and y (see diagram below).
2. Show that r(t) is a parameterization of the unit circle by showing it has constant length.
3. Explain why all but one point on the unit circle is the image of a point on the real line. What is that point?
4. Find the speed and arclength of r(t) for t in ( -¥,¥)

42. * Prove that the Cayley transform in exercise 41 is a 1-1 mapping.

43. The following is a parameterization of a circle in R³ for t in [ 0,p] :

r( t) =  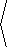 sin2( t) 1+sin2( t)  ,  sin( t) cos( t) 1+sin2( t)  ,  cos2( t) 2+2sin2( t)

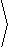What is its radius? (Hint: divide the length by 2p ).

44. Computer Algebra System: The following is the parameterization of a circle in R³ for t in [ 0,2p] .

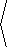
r( t) =  cos( t) 2cos2( t) +2cos( t) +1  ,  sin(t) 2cos2( t) +2cos( t) +1  ,  1+2cos( t) 2cos2( t) +2cos( t) +1

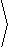What is its radius? (Hint: divide the length by 2p ).

45. Write to Learn: Write a short essay which explains why if a curve r is parameterized in terms of its arclength variable s, then its velocity is also its unit tangent vector for all s. (That is, the speed of the parameterization is identically 1).

46. Write to Learn: Suppose that r(t) = á f( t) ,g( t) ,h( t) ñ , t in [ a,b] parameterizes a curve C and suppose that f is a differentiable, 1-1 function. In section 1-6, exercise 44, we showed that

r( u) = á f( f( u) ),g( f( u) ) ,h( f( u) ) ñ ,  u  in  [ c,d]

parameterizes the same curve C when c = f^-1( a) and d = f^-1( b) . Write an essay explaining why the length of C is the same for both parameterizations.

47. Write to Learn: In section 1-5, we learned that circles can be parameterized by

r( t) = á p+Rcos( wt),q+Rsin( wt) ñ

where w is the angular speed of the parameterization. What is the arclength parameterization of r( t) ? What is the significance of the arclength parameter? How is the arclength reparameterization related to the parameterization

r( q) = á p+Rcos( q),q+Rsin( q) ñ

48. Suppose that r( t) is any curve that does not pass through the origin, and let

q( t) =  -k r r( t)

where k is a positive constant.

1. Show that q'  · q = 0 for all t. What is the significance of this result?
2. What is the speed of q( t) ?