Exercises

Find the velocity and acceleration of the following vector-valued functions:

1. r( t) = á t2,t3,t4 ñ 2. r( t) = át2,t5,t4 ñ 3. r( t) = át-1,t-2,t-3/2 ñ 4. r( t) = á ( t2-1) 1/2,( t2+1)-1,1 ñ 5. r( t) = á 3cos( t) ,5sin( t) ,4cos( t) ñ 6. r( t) = á 3cos( t) ,5sin( t),4cos( t) ñ 7. r( t) = á tan(t), cot(t), csc( t) ñ 8. r( t) = á et, e-t, ln( t2+1) ñ 9. r( t) = á 1,1,ln[ sec(t) ] ñ 10. r( t) = á 2,3,1 ñ et  - á 1,4,7 ñ e-t 11. r( t) = t2 i + tan-1( t) j 12. r( t) = i + t j + t2 k 13. r( t) = e-t á sin(t), cos( t), t ñ 14. r(t) = tan( t) á sin( t), cos(t), sec( t) ñ

Find the velocity at the given time and sketch it along with the curve r( t).

15. r( t) = á t2, t4 ñ,  t = 1 16. r( t) = á2t, 64-16t2 ñ , t = 1 17. r( t) = á cos(t), sin(t) ñ ,  t = p 6 18. r( t) = á cos(t), sin( t) ñ ,  t = p 6 19. r( t) = á et, e-t ñ,  t = 0 20. r( t) = á tan(t), sec( t) ñ ,  t = p 4 21. r( t) = á 3t+1,2t+3 ñ ,  t = 2 22. r( t) = á bt2,2bt ñ,  t = 1

Find the velocity v(t) and the position r(t) for the given acceleration and initial conditions, and determine the plane of motion (if it exists). In exercises 23 - 26, also find the time to maximum height, the maximum height, the time of impact, and the point of impact of the projectile (note: 27 and 28 are projectile motions with a small amount of atmospheric drag).

23. a(t) = á 0, 0,  -32 ñ 24.  a(t) = á 0, 0,  -32 ñ r0 = á 0,0,0 ñ, v0 = á 1,2,64 ñ r0 = á 0,0,0 ñ, v0 = á 1,1,96 ñ 25.  a(t) = á 0, 0,  -9.8 ñ 26.  a(t) = á 0, 0,  -9.8 ñ r0 = á 1,3,0 ñ, v0 = á 72,38,65 ñ r0 = á 2,1,3 ñ, v0 = á 1,1,0 ñ 27.  a(t) = á 0, 0,  -32 e -t/10  ñ 28.  a(t) = á 0, 0,  -32 e -t/20  ñ r0 = á 0,0,64 ñ, v0 = á 32,32,0 ñ r0 = á 0,0, 4 ñ, v0 = á 0,0,0 ñ 29. a(t) = á -3 sin(t), -5 cos(t), -4 sin(t)  ñ 30.  a(t) = á -3 sin(t), -3 cos(t), -12.2  ñ r0 = á 0,0,0 ñ, v0 = á 0,0,0 ñ r0 = á 0,0,0 ñ, v0 = á 0,0,0 ñ

31. In example 6 a projectile is moving near the surface of Mars, and we found that its position at time t is given by

r( t) = á 10t, 20t, 64t - 6.1t2 ñ

Find the plane of motion, the time to maximum height, the maximum height, the time of impact, and the point of impact of the projectile, and then compare the result to example 7, in which a projectile with the same initial conditions is traveling near the earth.

32. When r(0) is in the xy-plane, then the range of the projectile - i.e., the distance the projectile travels between leaving the earth and striking the earth - is the length of the vector r( t_imp) - r(0). That is,

range = || r( timp) - r(0)||

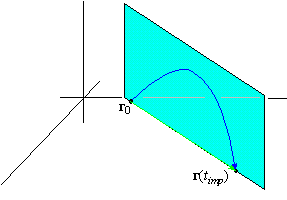
Find the range of the projectile in example 7, and then find the range of the projectile in problem 31. How much farther would the projectile travel on Mars than it would on the earth?

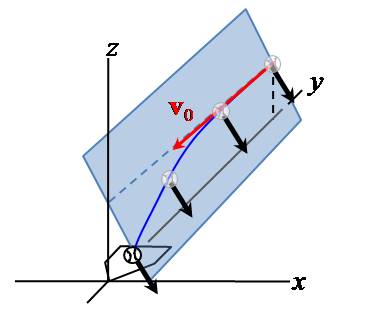
Exercises 33 - 38 explore Major League Baseball's "GameDay" pitch tracking system, in which the trajectory of a pitch is calculated using an imaging system, the coordinate system below, and projectile motion. Specifically, the Game Day pitch tracking system estimates the trajectory of a baseball in terms of a constant acceleration a (shown in black in the image above), a position r₀ when tracking begins (the beginning of the blue curve), and an initial velocity v₀  when tracking begins (40, 50, or 55 feet from the back of home plate).

33. On September 9, 2009 in a game between Anaheim and Seattle, Mark Jipsen through Ken Griffey, Jr., a sweeping curveball with the following GameDay vectors:

r0 = á -2.924, 50, 5.895 ñ,   v0 = á2.264, -121.647, -2.486ñ

a = á 10.529, 30.971, -41.439 ñ

Find the parameterization of the ball's trajectory r(t) by integrating a twice and using the given initial data. What is the plane of motion of the curveball? What is its position as it crosses the front of the plate ( i.e., when y=1.417 feet)? How much did it move from left to right

34. Repeat Exercise 33 for Mark Jipsen's last pitch of that game, which is

r0 = á -2.901, 50, 5.773 ñ,   v0 = á 8.42, -141.714, -4.76ñ

a = á -1.669, 36.404, -13.16 ñ

Is this also a curveball (in your opinion)?

35. On July 3, 2009 in a game between Minnesota and Detroit, Joel Zumaya threw a pitch clocked at well over 100 mph (and possibly the fastest pitch ever recorded -- a possible 105 mph when it left his hand at approximately y=55 feet). The data for that pitch is

r0 = á -1.901, 50, 5.928 ñ,   v0 = á 9.588, -147.939, -5.642ñ

a = á -15.819, 39.136, -6.834 ñ

How fast was the pitch traveling initially (i.e., when y=50 feet)? How long did it take to travel from y=55 (approximate point of release) to y=1.417 feet (the front of the plate)? How fast was it traveling when it crossed the front of the plate? (hint: 1 mile = 5280 feet).

36. Try it out! The data and information above can be obtained by beginning at Alan M. Nathan's website http://webusers.npl.illinois.edu/~a-nathan/pob/tracking.htm. Try finding the information above for an outing of your favorite pitcher and then repeating exercise 33.

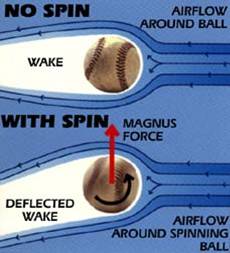
37. Magnus Force: The pitches in exercise 33 to 36 do not fall straight down because the spin of a baseball creates a force called the Magnus force which is perpendicular both to the direction of motion and to the axis about which the ball spins. For example, an angular velocity of about 1500 revolutions per minute induces a Magnus force which is about 1/3 the acceleration due to gravity -- i.e., about 11 feet per sec per sec! Drag must also be considered when Magnus force is considered, giving us an approximate acceleration of

a = á 11, 32, -32 ñ

Use this information to construct the trajectory of such a baseball given that

r0 = á 0, 50, 6 ñ,   v0 = á 0, -132, 0ñ

(i.e., ball 6 feet above the ground traveling 90 mph at 50 feet from the back of home plate).

38. Magnus Force Theory: In reality, the drag, magnus, and gravitational forces lead to an acceleration vector of the form

a = -KCDvv - KCLv ( w ×v)  - g

where K is a constant equalt to about 5.44×10^-3 per foot, v is the magnitude of the velocity v vector, g is the acceleration due to gravity, w is the unit vector parallel to the axis of rotation of the ball, and C_D and C_L are the drag and lift constants, respectively. Explain why a cannot be constant (i.e., the same at all times), and use this to explain why the Gameday curves are only statistical approximations and not actual physical trajectories. (more with Magnus force in later sections!)

39. When r₀ = á 0,0,0 ñ , projectile motion begins at the origin. Show that when r₀ = á 0,0,0 ñ , then t_imp = 2t_max.

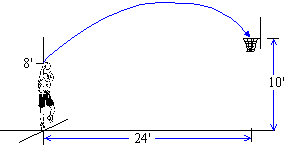
40. * A Basketball's Initial Velocity: An NBA player shoots a 3-pointer from 24 feet ( 3 point line is at 23'9''), and 1.4 seconds elapse before it passes through the hoop. If we assume that the player released the ball from a height of 8 feet, then what is the initial velocity of the ball? And what is the ball's maximum altitude?

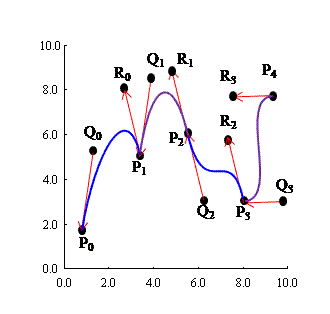
41. Bezier Curves: The Bezier curve determined by the 4 points P₀( x₀,y₀) , P₁(x₁,y₁) , P₂( x₂,y₂) , and P₃(x₃,y₃) is the curve with endpoints P₀ and P₃ which is tangent to the vectors P₀P₁ and P₂P₃ at the points P₀ and P₃, respectively.

(Click and drag the black "dots." Arrows drawn to 1/3 scale.)

In this exercise, we show that a Bezier curve is the graph of the vector valued function

r( t) = á x0,y0 ñt3 + 3 á x1,y1 ñ t2( 1-t) + 3 á x2,y2 ñ t( 1-t) 2  + áx3,y3 ñ ( 1-t) 3

for t in [ 0,1] .

1. Compute r( 0) and r( 1) .
2. Compute v( t) , and then compute v( 0) and v( 1) .
3. Explain how (a) and (b) relate to the figure shown above.

42. Bezier Curves: Construct the Bezier curve using the parameterization in exercise 39 using the 4 points P₀( 0,0) , P₁( 0,1) , P₂( 1,1) , and P₃(1,0) , and then sketch the result along with the vectors P₀P₁ and P₂P₃.

43. Write to Learn: Bezier curves are often used to connect a sequence of points (position vectors) P₀, P₁,…,P_{n} with a curve subject to a set of control points (position vectors) Q₀,…,Q_{n-1},R₀,…,R_{n-1}. Write short essay in which you show that for each j = 1,…,n, the curve

rj(t) = Pj-1t3 + 3Q1 ñ t2( 1-t) + 3 á x2,y2 ñ t( 1-t) 2  + áx3,y3 ñ ( 1-t) 3

for t in [0,1] satisfies r_{j}(0)=P_{j-1} and r_{j}(1)=P_{j}, as well as

r( u) = á f( f( u) ), g( f( u) ), h( f( u) ) ñ ,  u  in  [ c,d]

What conditions on P_{j}, R_{j-1} and Q_{j}, j=0,…,n-1, are necessary for the collection of "pieces" r₁(t),…,r_{n}(t) to form a smooth curve connecting all the points P₀, P₁, P₂,…,P_{n} .

r( u) = á f( f( u) ), g( f( u) ), h( f( u) ) ñ ,  u  in  [ c,d]

parameterizes the same curve C when c = f^-1( a) and d = f^-1( b) . What is the velocity vector for the new parameterization?  Is it the same as for the original parameterization?44. Write to Learn: Suppose that r(t) = á f(t), g(t), h(t) ñ , t in [ a,b] parameterizes a curve C and suppose that f is a differentiable, 1-1 function. Write a short essay explaining why

r( u) = á f( f( u) ), g( f( u) ), h( f( u) ) ñ ,  u  in  [ c,d]

parameterizes the same curve C when c = f^-1( a) and d = f^-1( b) . What is the velocity vector for the new parameterization?  Is it the same as for the original parameterization?