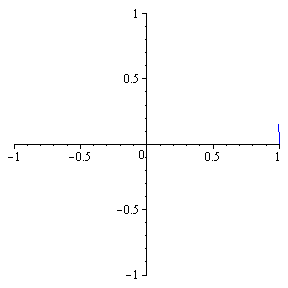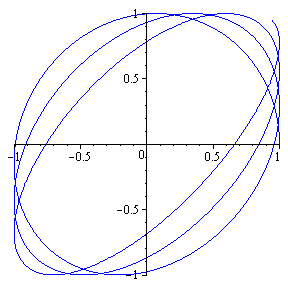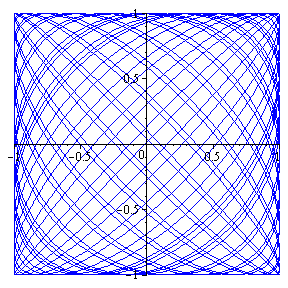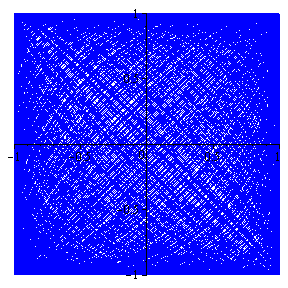Part 4:  Parametrizations in Which The Parameter Cannot Be Eliminated

Many oriented curves are not defined by a simple equation in x and y. For example, the curve

r(t) = á cos(3t), sin(pt) ñ,   t  in  [ 0, 120]

is much too complicated to be represented by a simple equation in x and y, as is shown below:

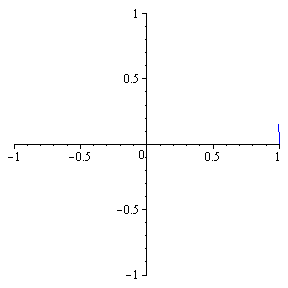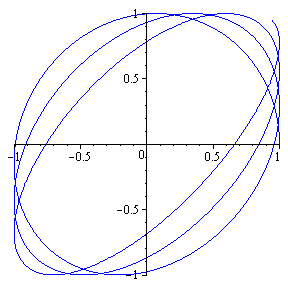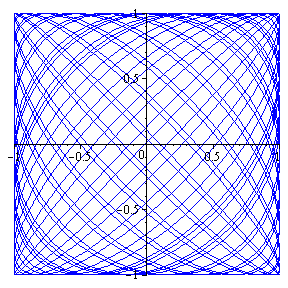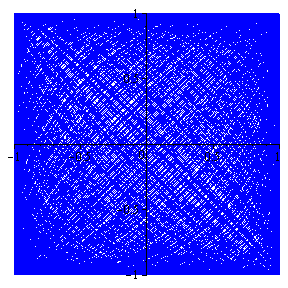click to toggle animation

Moreover, one of the most important oriented curves in mathematics-the cycloid-is a curve in which the parameter cannot be eliminated.       

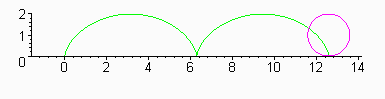
EXAMPLE 9    Find the parametric equations of a cycloid, which is the path traced out by a point on the edge of a wheel of radius R as it rolls along a horizontal path at a constant speed.

Click to toggle animation

Solution: To begin with, let us suppose that the point begins at the origin, and let us also suppose that x and y are the xy-coordinates of the point on the circle at time t. If q is the angle at time t formed by a radius to the point and a vertical line, then the point will have traveled a distance Rq at time t.

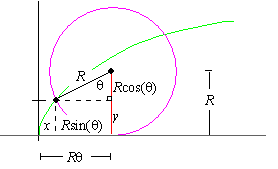
Moreover, the distance the center of the circle has moved will be the same as the distance the point on the rim has moved, so that the center of the circle will have moved a distance Rq horizontally at time t. The horizontal distance from the point to a vertical radius is Rcos(q) , so that

x + R sin(q) = Rq        Þ        x = Rq - R sin(q)

Similarly, the vertical distance from the horizontal line to the center is the sum of the y-coordinate and R sin(q) . However, since the radius of the circle is R, we must have

y + R cos(q)  =  R        Þ        y = R - R cos(q)

Finally, the center of the circle is moving at a constant speed, which implies that there is a constant w such that q = wt. Thus, the parametrization of a cycloid is given by

x   =   Rwt - R sin(wt) y   =   R - R cos(wt)

where R and w are constants.