Part 2: Using Identities to Eliminate the Parameter
In many instances, trigonometric identities are used to find the
equation in x and y corresponding to the graph of a given vector-valued
function. In particular, the following identities occur frequently in this
context:
In addition, we may also on occasion use identities such as 2sin(t) cos( t) = sin( 2t) and ete-t = 1.
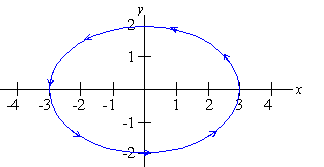
EXAMPLE 3 Sketch the curve
parameterized by r(t) =
á 3cos( t) ,2sin( t)
ñ for t in [ 0,2p] .
Solution: Since x = 3cos( t) and y = 2sin(t) , we begin with
Substituting cos( t) = x/3 and sin( t) = y/2
thus yields
If t = 0 or t = 2p, then x = 3 and y = 0. Thus, the initial and terminal
points are the same and correspondingly the graph of r(t) =
á 3cos( t) ,2sin( t)
ñ for t in [ 0,2p] is the entire ellipse
with counterclockwise orientation.
|
|
+ |
|
= 1 |
 |
|
A parameterization may trace a curve from the initial point to another point
and then may retrace the curve back to where it started, as we will see in
the next example. In this case, the orientation of the curve is not
well-defined.
EXAMPLE 4 Find the Cartesian equation and sketch the curve r( t) =
á cos( 2t) ,cos(t)
ñ for t in [ 0,2p] .
Solution: Since x = cos( 2t) and y = cos(t) , we use a double angle identity:
| cos( 2t) |
= |
2cos2( t) -1 |
| x |
= |
2y2-1 |
|
Moreover, r( 0) =
á cos( 0), cos( 0)
ñ =
á 1,1
ñ , r( p/2) =
á cos( p) ,cos( p/2)
ñ =
á -1,0
ñ , and r(p) =
á cos( 2p) , cos( p)
ñ =
á1,-1ñ. Also, r( 3p/2) =
ácos(3p),cos(3p/2)ñ =
á -1,0 ñ and r(2p) =
á cos( 4p) , cos(2 p)
ñ =
á1,1ñ. Thus,
the curve starts at ( 1,1) , progresses to ( -1,1) , and then retraces the curve in returning to ( 1,1) .
Consequently, the orientation is not well-defined.
EXAMPLE 5 Find the Cartesian equation of the curve
|
r( q) =
á 2sin(q) cos(q) ,2sin2( q)
ñ, q in [ 0,p] |
|
Solution: Since 2sin( q) cos( q) = sin( 2q) and 2sin2( q) = 1-cos( 2q) , we can rewrite r as
|
r( q) =
á sin( 2q),1-cos( 2q)
ñ |
|
which implies that x = sin( 2q) and y = 1-cos(2q) . Since
and since cos( 2q) = 1-y, we must have
Thus, r( q) =
á 2sin( q) cos( q), 2sin2( q)
ñ is a circle with radius 1 centered at ( 0,1) .
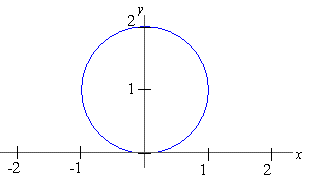
Check your Reading: What is the orientation of the curve
in example 5?
