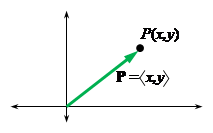Part 1: Equations of Lines
In this section, we use vectors, the cross product, and the dot
product to explore lines and planes in 3-dimensional space. We begin by
exploring the vector equation of a line in the xy-plane.
To begin with, a position vector is a vector P =
á x, y
ñ
whose initial point is fixed at the origin, so that each point P(x,y)
in R2 corresponds to a position vector
P =
á x, y
ñ.
(note: because a position vector cannot be translated, it is not really a
vector but should instead should be considered as a means of using the
arithmetic of vectors with points in the plane). Thus, a line corresponds to
the endpoints of a set of 2-dimensional position vectors.
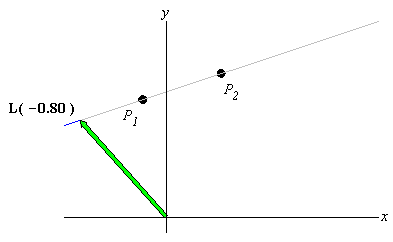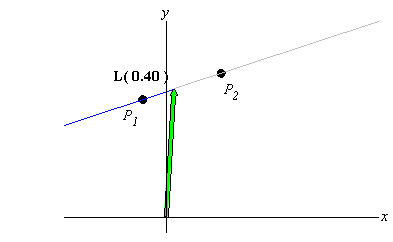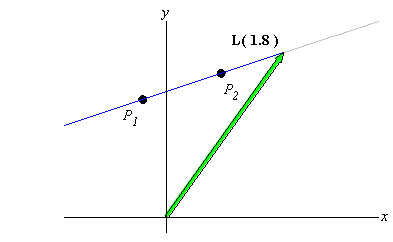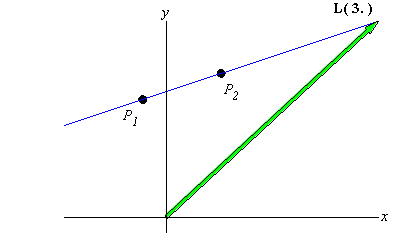
|
|
click image to toggle animation |
|
Indeed, if we define L(t) to be a
vector-valued function, which is a function that maps inputs t
to output vectors L(t), then a line in
2-dimensions is a vector-valued function of the form
where b is a fixed point ( = position vector) on the line and v is a
constant "slope" vector for the line.
The variable t is called a parameter, and it can be thought of as the "label" or "index"
of each point on the line. We use t for the parameter because in applications a point is often
labeled (i.e., indexed) by the time at which an object is
located at that point.
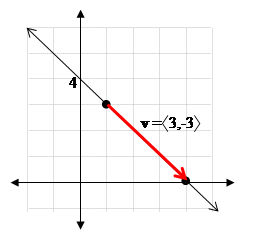
EXAMPLE 1 Find the
vector form of the line which passes through
the points P1( 1,3) and P2( 4,0), and
then determine the slope-intercept form of the line from the vector form.
Solution: To begin with, the vector v is given by
 |
 |
 |
|
v = |
P1P2
|
= á4 - 1, 0 - 3
ñ =
á 3,-3
ñ |
|
| |
As a result, the equation of the line is
|
L(t) = vt + b =
á3,-3
ñt +
á 1,3
ñ =
á 3t+1, -3t+3
ñ |
|
To find the slope-intercept form of the line, let us notice that the
x-coordinates are given by x = 3t + 1 and the y-coordinates are given by
y = -3t+3. Solving for t in the first equation yields
|
x- 1 = 3t and t = |
x - 1
3
|
|
Substituting into y = − 3t + 3 yields
|
y = -3 |

|
|
x -1
3 |
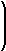 |
+ 3 = − ( x − 1) + 3 = − 3 x + 4
|
|
That is, y = 4 − 3x is the slope-intercept form of the
line.
The advantage of a vector equation of a line over point-slope and
slope-intercept forms of a line is that a vector equation generalizes to 3
or more dimensions, whereas slope-based forms of a line do not.
Indeed, if we notice that each point P( x,y,z)
in R3 corresponds to a 3-dimensional position vector P
= á x, y, z ñ.
then a line in 3-dimensional space through two points ( = position vectors )
P1 and P2
is of the form
where v is the vector from P1 to P2 and b is the
position vector of a point on the line (such as b = P1 ).
A physical interpretation of (1) is
that if an object moves along the line L(t) at a constant speed equal to the magnitude of v,
then t would be the time at which the object is located at point L(t) on the line.
EXAMPLE 2 Find the equation of the line which passes through
the points P1( 1,0,1) and P2( 4,3,2) , and
interpret the result given that an object is located at point P1 at time t = 0 sec and at point
P2 at time t = 1 sec.
Solution: The vector v is given by
 |
 |
 |
|
v = |
P1P2
|
= á4-1,3-0,2-1
ñ =
á 3,3,1
ñ |
|
| |
As a result, the equation of the line is
|
L(t) = P1+tv =
á1,0,1
ñ +t
á 3,3,1
ñ |
|
which reduces to L( t) =
á3t+1,3t,t+1
ñ . For example, t = 0 and t = 1 yields
|
L( 0) =
á 1,0,1
ñ = P1 and L( 1) =
á 3( 1) +1,3(1) ,1+1
ñ =
á 4,3,2
ñ = P2 |
|
Other points on the line follow from other choices of t. For example, when
t = 2, we obtain the position vector
|
L( 2) =
á 3( 2) +1, 3(2), 2+1
ñ =
á 7,6,3
ñ |
|
Likewise, when t = -1, we obtain the position vector L(-1) =
á -2,-3,0
ñ , which corresponds to the
point P0( -2,-3,0) .
Finally, we can obtain an especially useful form of a line if we notice that v = P2-P1. Substituting into (1) leads
to L( t) = P1+t( P2-P1) , which reduces to
Clearly, L( 0) = P1 and L(1) = P2,
so that L(t) with 0 £ t £ 1 is the line segment with endpoints P1 and P2. Moreover, (2) shows that the order of the
points is not important in the equation of a line.
Check your Reading: What is the parameter for
a line with vector equation K( s) = m s
?