Part 3: Vector Arithmetic

The parallelogram law (which we prove in the exercises) says that the sum u+v is the main diagonal of the parallelogram formed by u and v. In addition, the difference of 2 vectors is

u - v = á u1-v1,u2-v2,u3-v3 ñ

which corresponds to the off-diagonal of the parallelogram defined by u and v.

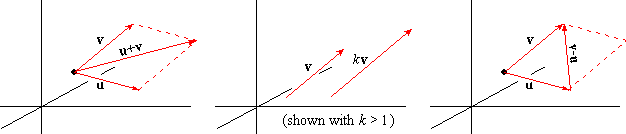
If u = kv for some nonzero scalar k, then u and v are said to be scalar multiples of each other. Geometrically, if u and v are scalar multiples of each other, then u and v are said to be parallel.

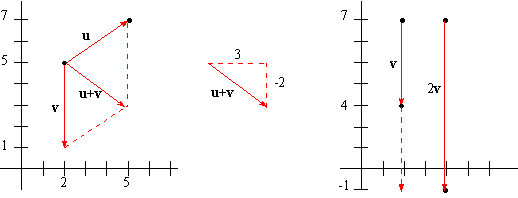
EXAMPLE 6    Find u+v and 2v when u = á 3,2 ñ and v = á0,-4 ñ       

Solution: Their sum is given by

u+v = á 3,2 ñ + á 0,-4 ñ = á 3+0,2-4 ñ = á 3,-2 ñ

Moreover, multiplication of v = á 0,-4 ñ by the scalar 2 yields

2v = 2 á 0,-4 ñ = á 0,-8 ñ

The sum and scalar multiplication are shown geometrically below:

       

The 0 vector is defined 0 = á 0,0,0 ñ . It is shown in the exercises that the arithmetic of vectors has the following properties:

Theorem 1.1: If u, v, w are vectors and if k, m are scalars, then

(1) u+v = v+u (5) k( u+v) = ku+kv (2) u+0 = u (6) ( k+m) u = ku+mu (3) u+( v+w) = ( u+v) +w (7) ( km) u = k ( mu) (4) u-v = u+( -v)

 The properties in Theorem 1.1 and the concepts of magnitude and direction allow vectors to be used in many different applications.

EXAMPLE 7       An airplane heads due east at 200 mph through a crosswind blowing due north at 30 mph.  The superposition (i.e., sum) of these two velocities is the airplane's actual velocity vector. What is the airplane's actual speed and direction?

Solution: The heading velocity vector is á200,0 ñ and the wind velocity vector is á0,30 ñ .  Thus, the actual veclocity of the airplane is

v = á 200,0 ñ + á 0,30 ñ = á 200, 30 ñ

which is the main diagonal of the parallelogram (in this case, a  rectangle) formed by the heading and wind vectors.
The airplane's actual speed is the magnitude of v:

||v|| =   2002 + 302   =  202.24  mph

The actual direction can be found from the fact that ||v|| cos(a) = a, which in our case yields

202.24 cos(a) = 200, or  a = cos-1 æ ç è 3 202.24   ö ÷ ø  = 0.588 radians

This is about a = 0.14897( 180/p) = 8.5354^° north of due east.

In general, a vector is an element of a Vector Space, where a Vector Space is a set with addition and scalar multiplication operations satisfying (1) - (7) in theorem 1.1. For example, R³ is the vector space of all possible 3-dimensional vectors, and a given vector v = áa,b,cñ  is an element in the vector space R³.