The Divergence Theorem and Differential Forms

Let's show that Stoke's theorem can be extended to include integrals over solids and their boundary surfaces. To begin with, in terms of C^¥ functions x( u,v,w) , y( u,v,w) , and z( u,v,w) , a wedge product of a wedge product is defined

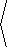
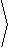
dx^dy^dz = á xw,yw,zw ñ ·    ¶( y,z) ¶( u,v) ,    ¶( z,x) ¶(u,v) ,    ¶( x,y) ¶( u,v) dudv dw

It is not difficult to show that this definition extends the wedge product in a natural way-that is, that dx^dz^dy = -dx^dy^dz, dx^dx^dz = 0, and similar for similar expressions.

For example, if x( u,v) and y( u,v) are functions of u and v and if z = w, then

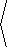
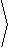
dx^dy^dz = á 0,0,1 ñ ·    0, 0,    ¶( x,y) ¶( u,v) dudv dw

However, w = z and the fact that the latter term is dA implies that

dx^dy^dz = dz  dA

which is the volume differential dV for the solid between two surfaces z = p( x,y) and z = q( x,y) over a region R.

Consequently, 3-forms, which are also known as volume forms, are defined

U( x,y,z) dx^dy^dz

where U( x,y,z) is a 0-form. We also define the differential of a 2-form w = Mdy^dz+Ndz^dx+Pdx^dy to be

dw = dM^dy^dz+dN^dz^dx+dP^dx^dy

where dM, dN, and dP are differentials of the 0-forms M, N, and P, respectively.

For example, if F = á M,N,P ñ is a vector field and dS = á dy^dz,dz^dx,dx^dy ñ is the vector surface differential of the boundary of a solid, then

F·dS = M( x,y,z) dy^dz+N(x,y,z) dz^dx+P( x,y,z) dx^dy

and differential of F·dS is thus given by

d( F·dS)  =  d ( Mdy^dz+Ndz^dx+Pdx^dy)  =  dM^dy^dz+dN^dz^dx+dP^dx^dy

Let's calculate d( F·dS) . Since dM = M_xdx+M_ydy+M_zdz, we have

dM^dy^dz  =  ( Mxdx+Mydy+Mzdz) ^( dy^dz)  =  Mxdx^dy^dz+Mydy^dy^dz+Mzdz^dy^dz  =  Mxdx^dy^dz+0-Mzdy^dz^dz  =  Mxdx^dy^dz

Similarly, all but one term in each of dN^dz^dx and dP^dx^dy vanishes, so that

d( F · dS) = Mxdx^dy^dz+Nydy^dz^dx+Pzdz^dx^dy

Finally, dy^dz^dx = -dy^dx^dz = dx^dy^dz and similarly, dz^dx^dy = -dx^dz^dy = dx^dy^dz, so that

d( F · dS)  =  Mxdx^dy^dz+Nydx^dy^dz+Pzdx^dy^dz  =  ( Mx+Ny+Pz) dx^dy^dz

which is to say that d( F·dS) = div( F) dV. If we use this in the divergence theorem, then we obtain

ó õ ó õ ¶S  F · dS = ó õ ó õ ó õ S  div( F) dV = ó õ ó õ ó õ S  d( F · dS)

That is, the divergence theorem is simply Stoke's theorem again, since if w = F · dS, then dw = d( F · dS) .      

Stoke's Theorem: If S is a solid bounded by a surface ¶S and if w is a 2-form, then

ó õ ó õ ¶S  w = ó õ ó õ ó õ S  dw

Let's look at an example.     

EXAMPLE 4    Suppose S is the cuboid [ 0,1] ×[ 0,1] ×[ 0,1] . Apply Stoke's theorem to

ó õ ó õ ¶S  y  dy^dz+xz2dx^dy

Solution: The boundary of the unit cube is a surface with 6 square faces, so that direct evaluation of the integral would require 6 separate flux integrals. However, Stoke's theorem implies that

ó õ ó õ ¶S  y  dy^dz+xz2dx^dy  =  ó õ ó õ ó õ S  d( y  dy^dz+xz2dx^dy)  =  ó õ ó õ ó õ S  dy^dy^dz+d( xz2) ^dx^dy  =  ó õ ó õ ó õ S  z2dx^dx^dy+2xz  dz^dx^dy  =  ó õ ó õ ó õ S  2xz  dx^dy^dz

Since dV = dx^dy^dz, this leads to

ó õ ó õ ¶S  y  dy^dz+xz2dx^dy  =  ó õ ó õ ó õ S  2xz  dV  =  ó õ 1 0  ó õ 1 0  ó õ 1 0  2xz  dzdydx  =  1 2

       

EXAMPLE 5    Let S be the solid inside the cylinder x²+y² = 1 for z in [ 0,1] . Evaluate

ó õ ó õ ¶S  z  dx^dy

Solution: Recall that dz^dy^dx = dx^dy^dz = dV, so that

ó õ ó õ ¶S  z  dx^dy = ó õ ó õ ó õ S  dz^dx^dy = ó õ ó õ ó õ S  dV

Since the solid is between z = 0 and z = 1 over the unit disk, D, we have

ó õ ó õ ¶S  z  dx^dy = ó õ ó õ D ó õ 1 0  dzdA = ó õ ó õ D dA = ó õ 2p 0  ó õ 1 0  rdrdq = p