Because theorems 2 and 3 both involve the work integral, these
theorems are important throughout mathematics and science.
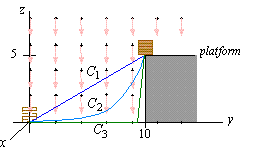
EXAMPLE 7 How much work is performed in moving a box with a
mass of 1 slug from the origin to the point (0,10 feet,5 feet) through the gravitational force field F( x,y,z
) =
á 0,0,-32
ñ along each of the
curves C1, C2, and C3 shown below?
Solution: First, let's use theorem 3 to show that F is a
conservative field. If C is a closed curve in R3 parametrized by r( t) =
á x( t) ,y( t),z( t)
ñ , t in [ a,b] , then
|
| 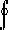 |
C
|
F·dr = |
ó
õ
|
b
a
|
F· |
dr
dt
|
dt = |
ó
õ
|
b
a
|
á 0,0,-32
ñ · |
|
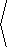
|
dx
dt
|
, |
dy
dt
|
, |
dz
dt
| 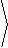 |
dt |
|
Since C is a closed curve, r( a) = r(b) , which implies that z( a) = z( b) . Thus,
|
| 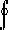 |
C
|
F·dr = -32 |
ó
õ
|
b
a
|
|
dz
dt
|
dt = -32[ z( b) -z( a) ] = 0 |
|
Thus, 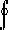 CF·dr = 0 for any closed curve C,
which by theorem 3 implies that F is conservative.
CF·dr = 0 for any closed curve C,
which by theorem 3 implies that F is conservative.
Indeed, it is easy to show that F has a potential of
As a result, the work performed in moving an object from (0,0,0) to ( 0,10,5) is U( x,y,z) = -32z+k,
so that using theorem 1 we also have
|
W = |
ó
õ
|
( 0,10,5)
( 0,0,0)
|
F·dr = -32z+k |
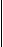 |
(0,10,5)
( 0,0,0) |
= -160 |
slug ft2
sec2
|
|
|
Moreover, path independence implies that the work is W = -160 slug-ft2/sec2 along any path from ( 0,0,0) to (0,10,5) , so that specifically, the work along each of the three
curves C1, C2, and C3 is -160 slug-ft2/sec2.

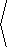
CF·dr = 0 for any closed curve C, which by theorem 3 implies that F is conservative.