Part 2: The Fundamental Theorem of Calculus

Now let's use line integrals, vector fields, and potential functions to generalize the Fundamental Theorem of Calculus. Let's suppose that C is a curve parametrized by r( t) = áx( t) ,y( t) ñ for t in [a,b] , and let's suppose that C is in an open simply connected region R on which F( x,y) = á M(x,y) ,N( x,y) ñ is a conservative vector field. The line integral of F( x,y,z) over C is given by

ó õ C  F·dr = ó õ C  á M,N,P ñ· á dx,dy,dz ñ = ó õ C  Mdx+Ndy+Pdz

Moreover, F conservative implies that there is a function U( x,y,z) such that M = U_x , N = U_y, and P = U_z. As a result, reduction of the line integral to the parameter t yields

ó õ C  Mdx+Ndy+Pdz = ó õ b a  æ è M  dx dt +N  dy dt +P  dz dt ö ø   dt = ó õ b a  æ è  ¶U ¶x  dx dt +  ¶U ¶y  dy dt +  ¶U ¶z  dz dt ö ø   dt

However, the chain rule says that the integrand is dU/dt, so that

ó õ C  F·dr = ó õ b a   dU dt dt = U( r( t) ) |   b a  = U( r( b) ) -U( r( a) )

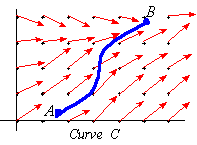
Indeed, if we let A and B denote the initial and final points of the curve C, then we have shown the following:       

Theorem 2: If F( x,y,z ) = á M(x,y,z) ,N( x,y,z) ,P( x,y,z) ñ is a conservative vector field over an open simply connected region R with potential U( x,y,z) , and if C is a curve in R beginning at A and ending at B, then

ó õ C  F·dr = U( B) - U( A)

       

Equivalently, theorem 2 can be expressed in the form

ó õ C  Mdx+Ndy+Pdz = U( B) - U( A) .

or in the form ò_C ÑU·dr = U( B) -U(A) .       

EXAMPLE 3    Suppose that C begins at ( 0,0 ) and ends at ( 1,3) . If  F( x,y) =   á 2x+y, x-4y ñ , then what is the value of the line integral

ó õ C    F · dr

Solution: The vector field has a potential of U( x,y,z) = x² + xy - 2y² + k  (see example 1). Thus,

ó õ C  F · dr   =   x2 + xy - 2y2  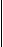( 1,3) (0,0)   =  ( 12 + 1·3 - 2·32) -0    =  -14

 

EXAMPLE 4    Suppose that C begins at ( 0,0,0 ) and ends at ( 1,2,3) . What is the value of the line integral

ó õ C    yzdx+( xz+2y) dy+( xy+1) dz

Solution: The vector field is F( x,y,z) =   á yz,xz+2y,xy+1 ñ , which has a potential of U( x,y,z) = xyz+y²+z+C₁ (see example 2). Thus,

ó õ C  yzdx+( xz+2y) dy+( xy+1) dz   =   xyz+y2+z  ( 1,2,3) (0,0,0)   =  ( 1·2·3+22+3) -0   =  13