Part 1: Finding Potentials

Line integrals are important in applications because they allow us to generalize the fundamental theorem of calculus to higher dimensional settings. Let's examine such a generalization in this section by considering line integrals in conservative vector fields.

Theorem 1 in section 1 says that if curl( F) = 0, then F is conservative (or equivalently, exact), which is to say that there is a function U( x,y,z) such that

ÑU( x,y,z) = F( x,y,z)

For a 2 dimensional vector field F( x,y) = áM( x,y) ,N( x,y) ñ , the curl of F reduces to

curl  F = á 0,0,Nx-My ñ

(1)

If N_x = M_y, in which case F  = á M,N ñ is exact, then there is a function U( x,y) such that U_x = M and U_y = N. Integration of M with respect to x leads to

U( x,y) = ó õ M( x,y) dx+C(y)

where C is a function of y because y is considered constant when integrating with respect to x. To determine C( y) , we calculate U_y , set it equal to N, and integrate.       

EXAMPLE 1    Test to determine if the vector field F( x,y) = á2x+y, x-4y ñ is conservative. If it is, find its potential.       

Solution: Since M = 2x+y and N = x-4y, the curl of F is

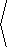curl  F = 0, 0,   ¶ ¶x (x-4y) -  ¶ ¶y ( 2x+y) 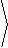= á 0,0,1-1 ñ = á 0,0,0 ñ

To find its potential, we first integrate M = 2x+y with respect to x:

U( x,y) = ó õ ( 2x+y) dx = x2+xy+C( y)

We then determine C( y) by setting U_y = x+C^¢(y) equal to N:

x+C' ( y) = x-4y        Þ        C' ( y) = -4y

Thus, C( y) = ò-4ydy = -2y²+k, where k is constant, and the potential of F is

U( x,y) = x2+xy-2y2 + k

       

If a 3-dimensional vector field F = áM,N,P ñ is conservative, then we find its potential in much the same way we did for 2 variables. In particular, we compute

U( x,y,z) =  ó õ M( x,y,z ) dx+C(y,z)

where the constant is now a function of both x and y. We set U_y equal to N to determine C. Having done so, we compute U_z and set it equal to P to finish calculating U( x,y,z) .       

EXAMPLE 2    Determine if the vector field F(x,y,z) =   á yz, xz+2y, xy+1 ñ is conservative. If it is, find its potential       

Solution: Since M = yz, N = xz+2y, and P = xy+1, we have

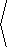
curl  F =  ¶ ¶y (xy+1) -  ¶ ¶z ( xz+2y) ,  ¶ ¶z ( yz) -  ¶ ¶x (xy+1) ,  ¶ ¶x ( xz+2y) -  ¶ ¶y ( yz) 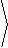= á x-x,y-y,1-1 ñ = á 0,0,0 ñ

Thus, F is conservative. To find its potential, we integrate M with respect to x.

U = ó õ yzdx = xyz+C( y)

Differentiating with respect to y and setting U_y equal to N then yields

Uy = xz+C' ( y) = xz+2y = N        Þ        C' ( y) = 2y

Thus, C( y) = y²+k( z) and as a result, we now have U( x,y,z) = xyz+y²+k( z) . Finally, U_z = xy+k' ( z) , so that setting U_z equal to P = xy+1 yields

xy+k' ( z) = xy+1 k' ( z) = 1 k( z) = z+C1

so that the potential is U( x,y,z ) = xyz + y² + z + C₁ where C₁ is a constant.