Part 4: Properties of Line Integrals

The usual properties of integration also hold for line integrals, such as

ó õ C  ( F+G) ·dr = ó õ C  F·dr+ ó õ C  G·dr ó õ C  kF·dr = k ó õ C  F·dr

where k is a constant. Moreover, if r( t) , t in [ a,b] , parametrizes a curve C, then the arclength parametrization is of the form r( t( s) ) for s in [ a,b] . It then follows that

ó õ C  F·dr = ó õ b a  F·  dr dt dt = ó õ b a  F·  dr dt  dt ds ds = ó õ b a    F·  dr ds   ds

(7)

That is, the line integral over any parametrization of C can be transformed into an integral over the arclength parameter, thus implying that any two different parametrizations of C yield the same value for the line integral.

Indeed, the properties of line integrals closely resemble the properties of ordinary integrals. For example, if C₁ is a curve that begins at A and ends at P, and if C₂ is a curve that begins at P and ends at B, then their union is defined to be the curve C₁ÈC₂ that progresses along C₁ from A to P and then along C₂ from P to B:

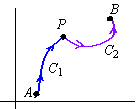
It is straightforward to show that

Moreover, if C is a curve parametrized by r( t) = á x( t) ,y( t) ñ , t in [ a,b] , then the curve -C is the curve parametrized by r( t) = á x( -t) ,y( -t) ñ , t in [ -b,-a] , and consequently, is the same as C but with the opposite orientation.

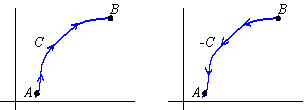
It is also straightforward to show that

EXAMPLE 7    If C is the union of two curves C₁ and C₂, and if

ó õ C1  F ·dr = 3,        ó õ C2  F·dr = 7

then what is ò_-C  F·dr?   

Solution: To begin with, we must have

ó õ -C  F·dr = - ó õ C  F·dr

Moreover, since C = C₁ÈC₂, we further have

ó õ -C  F·dr = - ó õ C1ÈC2  F·dr = - é ë ó õ C1  F·dr+ ó õ C2  F·dr ù û = -( 3+7) = -10