One of the most important ideas in mathematics is the concept of a vector field. In this section, we introduce vector fields and describe some of their applications.
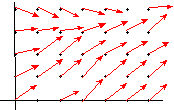
To begin with, a vector field on the xy-plane is a mapping F( x,y) = á M( x,y) ,N( x,y) ñ which assigns the vector á M,N ñ to each point ( x,y) in the plane. To visualize vector fields, we often define a grid of points and then draw the vector F(x,y) with initial point at a point ( x,y) in the grid.

Unfortunately, such diagrams can become quite cluttered, so it is not unusual for the actual vectors F( x,y) to be drawn much shorter than actual length.
EXAMPLE 1 Sketch the vector field F( x,y) = á x+y, x-y ñ on the grid shown below:
Solution: Notice that F( 0,1) = á0+1,0-1 ñ = á 1,-1 ñ . Thus, we draw the vector á 1,-1 ñ at the point (0,1) . Likewise, F( 0,2) = á 2,-2 ñ , F( 1,2) = á 3,-1 ñ , and F( 1,1) = á 1+1,1-1 ñ = á2,0 ñ , so that we draw the vector á2,-2 ñ at the point ( 0,1) , we draw the vector á 3,-1 ñ at ( 1,2) , and we draw the vector á 2,0 ñ at the point ( 1,1) .
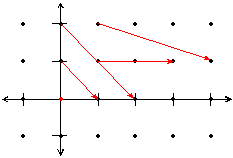
Unfortunately, if we draw all the vectors implied by the grid points, the diagram would become quite cluttered. Thus, we scale all of the vectors. In the figure below, each vector has been scaled by 1/4:
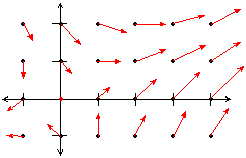
Since F( 0,0) = á 0,0 ñ , we place a red dot at the origin to signify the zero vector.
Similarly, a 3 dimensional vector field is a mapping
|
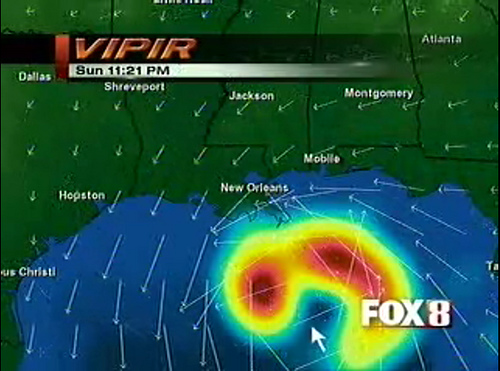
Vector fields are important in many real-world applications. For example, check out some of the following links.
| Hurricane Wind Vector Field: | http://people.eecs.ku.edu/~miller/WorldWind/ | |
| Real time radar Vector Fields: | http://marine.rutgers.edu/mrs/codar/real-time/real_time.html | |
| Magnetic Vector Field: | http://web.mit.edu/jbelcher/www/java/part_biot/part_biot.html | |
| Animated Dipole: | http://webphysics.davidson.edu/opensourcephysics/applets/osp3d/dipole1.html | |
| Solar Vector Field (Click on Animation) | http://solarscience.msfc.nasa.gov/flaremag.shtml | |