Part 4: Moments and Centers of Mass

If a solid S has a mass density of m( x,y,z) , then its first moments are defined to be

Myz =  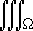 xm( x,y,z) dV,    Mxz =  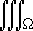ym( x,y,z) dV

Mxy =  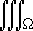 zm( x,y,z) dV

Since the mass of S is given by

M =  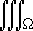m( x,y,z) dV

the moments allow us to generalize the concept of center of mass to arbitrary solids. In particular, the center of mass of a solid with mass density m( x,y,z) is defined to be the point in R³ with coordinates

x  =   Myz M ,    y  =   Mxz M ,    z  =   Mxy M

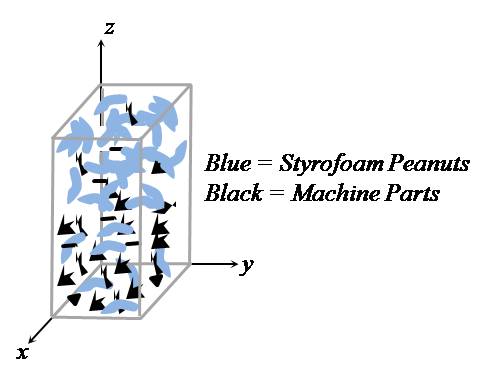
EXAMPLE 4    Find the center of mass of the mixture in example 3 -- i.e., of the styrofoam peanuts/machine parts mixture in the box [ 0,1] ×[ 0,1] ×[ 0,2] with a mass density of a density of

m( x,y,z) = ( 9-z3)    kg m3

Solution: The moments of the box in example 3 are given by

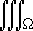Myz =  x  m( x,y,z)dV = ó õ 1 0  ó õ 1 0  ó õ 2 0  ( 9-z3) x dzdydx 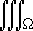Mxz =  y  m( x,y,z)dV = ó õ 1 0  ó õ 1 0  ó õ 2 0  ( 9-z3) y dzdydx 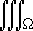Mxy =  z  m( x,y,z)dV = ó õ 1 0  ó õ 1 0  ó õ 2 0  ( 9-z3) z dzdydx

Evaluating these integrals and computing the coordinates of the center of mass yields

Myz = 7  kg·m,        - x   =  7 14 = 0.5  m Mxz = 7  kg·m,        - y   =  7 14 = 0.5  m Mxy = 11.6  kg·m,        - z   =  11.6 14 = 0.83  m

Thus, the center of mass is ( 0.5, 0.5, 0.83) .

That is, the settling of the heavier parts toward the bottom implies a lower center of mass than would have been expected if the parts and peanuts had remained uniformly mixed.    

The first moments of a solid W with a mass density m( x,y,z) are used to determine the center of mass of the solid.  Higher moments - moments with nonlinear expressions in x, y, and z are also important, as they are used to reveal other properties of a solid.   For example, the moments of inertia about the three coordinate axes are

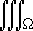Ix = ( y2+z2) m( x,y,z)dV,      Iy =   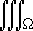 ( x2+z2) m(x,y,z) dV 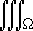Iz = ( x2+y2) m( x,y,z) dV

Moments of inertia are the rotational analogs of mass.  For example, the angular momentum of an object rotated about the z-axis is L = I_z w, where w is angular velocity.

EXAMPLE 8    What is the moment of inertia about the z-axis of the machine parts, styrofoam peanuts mixture in example 3, where the mass density is

m( x,y,z) = ( 9-z3)    kg m3

for the solid [ 0,1] ×[ 0,1] ×[ 0,2] .

Solution: The moment of inertia about the z-axis is

Iz = [ 0,1] ×[ 0,1] ×[ 0,2]    ( x2+y2) m( x,y,z) dV = ó õ 1 0  ó õ 1 0  ó õ 2 0  ( x2+y2) (9-z3) dzdydx = ó õ 1 0  ó õ 1 0  ( x2+y2) æ è 9z-  z4 4 ö ø ê ê 2 0  dydx = ó õ 1 0  ó õ 1 0  17( x2+y2) dydx = 17 ó õ 1 0  x2y+  y3 3 ê ê 1 0  dx = 17 ó õ 1 0  æ è x2+  1 3 ö ø dx = 17 æ è  2 3 ö ø   m2·kg