Exercises

Find and describe the image of the given region under the given transformation. Then compute the area of the image.

1. T( u,v) = á 2u,4v ñ 2. T( u,v) = á u+3,2v ñ S = [ 0,1] × [ 0,1] S = [0,1] × [ 0,1] 3. T( u,v) = á u,2u+v ñ 4. T( u,v) = á u-v,u+v ñ S = [ 0,1] × [ 0,1] S = [0,1] × [ 0,1] 5. T( u,v) = á u2-v2,2uv ñ 6. T( u,v) = á u-v,uv ñ S = [ 0,1] × [ 0,1] S = [0,1] × [ 0,1] 7. T( u,v) = á 4ucos( v) ,3usin(v) ñ , 8. T( u,v) = á ucosh( v), usinh( v) ñ , S = [ 0,1] × [ 0,2p] S = [0,1] × [ 0,1]

Use the given transformation to evaluate the given iterated integral.

9. ó õ 1 0  ó õ 2 0   2xy x2+1 dydx 10. ó õ 1 0  ó õ 1 0  xysin( y2) dydx T( u,v) = á Öu,v ñ T( u,v) = á u,Öv ñ 11. ó õ 1 0  ó õ 1 0  excos( ex) dxdy 12. ó õ 1 0  ó õ 1 0  cos( y) esin( y) dydx T( u,v) = á ln( u) ,v ñ T( u,v) = á u,sin-1( v) ñ 13. ó õ 1 0  ó õ x 0  cos( x2) dydx 14. ó õ 1 0  ó õ 1 x  cos( y2) dydx T( u,v) = á v,u ñ T(u,v) = á v,u ñ

15. ó õ 2 1  ó õ 2x+3 2x+1     1 2y-4x dydx 16. ó õ 1 0  ó õ 2x+1 2x    y-2x   dydx T( u,v) = á u,2u+v ñ T(u,v) = á u,2u+v ñ 17. ó õ 1 0  ó õ y+1 y-1   sin( y-x) dxdy 18. ó õ 2 1  ó õ y+1 y     dxdy xy-y2 T( u,v) = á u+v,v ñ T(u,v) = á u+v,v ñ 19. ó õ 1 0  ó õ 1 y   sin( π x2) dxdy 20. ó õ 1 0  ó õ 2x x  ex2dydx T( u,v) = á u,uv ñ T(u,v) = á u,uv ñ 21. ó õ ó õ R  Ö xy dA, 22.   ó õ xy3  dA, T( u,v) =  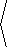u v , uv 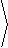T( u,v) =  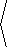u v ,uv 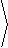R bounded by xy = 1, xy = 9 R bounded by xy = 1, xy = 9 y = x, y = 4x y = x, y = 4x

Use the given transformation to transform the given iterated integral. Then reduce to a single integral and approximate numerically.

23. ó õ 1 0  ó õ x -x  cos[ ( x-y) 2]dydx 24. ó õ 1 0  ó õ x -x  cos[ ( x+y)2] dydx T( u,v) = á v+u,v-u ñ T(u,v) = á v+u,v-u ñ 25. ó õ 1 -1  ó õ Ö 1-x2 0   sin(x2+y2) x2+y2 dydx 26. ó õ 1 -1  ó õ 0.5 Ö 1-x2 0   sin( x2+4y2) x2+4y2 dydx T( u,v) = á vcos( u) ,vsin(u) ñ T( u,v) = á 2vcos( u) ,vsin( u) ñ 27. ó õ 2 0  ó õ 1-y2/4 y2/4-1  ln(16x2-8xy2+y4+1) dxdy  28. ó õ 2 0  ó õ 1-y2/4 y2/4-1  e16x2-8xy2+y4dxdy T( u,v) = á u2-v2,2uv ñ T( u,v) = á u2-v2,2uv ñ

29. Evaluate the following iterated integral in two ways:

ó õ 1 0  ó õ 3 0  2xcos( x2) dxdy

1. By letting w = x², dw = 2xdx and noting that x = 0 implies w = 0 while x = 3 implies w = 9.
2. Using the coordinate transformation

   T( u,v) = á Öu,v ñ

30. Evaluate the following iterated integral in two ways:

ó õ 1 0  ó õ 4 0  Öxcos( Öx ) dxdy

1. By letting w = Öx, dw = dx/( 2Öx) and noting that x = 0 implies w = 0 while x = 4 implies w = 2.
2. Using the coordinate transformation

   T( u,v) = á u2, v ñ

31. In two different ways, we show that if g is a differentiable function, then

ó õ b a  ó õ g( d) g( c)   f(x,y) dydx = ó õ b a  ó õ d c  f( u,g( v)) g' ( v) dvdu

1. By letting y = g( v) , dy = g' ( v) dv in the rightmost iterated integral.
2. By considering the coordinate transformation T( u,v) = á u,g( v) ñ .

32. In two different ways, we show that if f is a differentiable function, then

ó õ f( b) f( a)   ó õ g( d) g( c)  f( x,y)dydx = ó õ b a  ó õ d c  f( f( u) ,g( v)) f ' ( u) g' ( v) dvdu

1. By letting x = f( u) ,dx = f^¢( u) du and y = g( v) , dy = g' ( v) dv in the rightmost iterated integral.
2. By considering the coordinate transformation T( u,v) = á f( u) ,g( v) ñ

33. The parabolic coordinate system on the xy-plane is given by

T( u,v) = á u2-v2,2uv ñ

If T maps a region S in the uv-plane to a region R in the xy-plane, then what does the change of variable formula imply that

ó õ ó õ R  f( x,y) dA

will become when integrated over S in the uv-coordinate system?

34. The tangent coordinate system on the xy-plane is given by

T( u,v) =  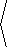u u2+v2 ,  v u2+v2

If T maps a region S in the uv-plane to a region R in the xy-plane, then what does the change of variable formula imply that

ó õ ó õ R  f( x,y) dA

will become when integrated over S in the uv-coordinate system?

35. The elliptic coordinate system on the xy-plane is given by

T( u,v) = á cosh( u) cos( v), sinh( u) sin( v) ñ

If T maps a region S in the uv-plane to a region R in the xy-plane, then what does the change of variable formula imply that

ó õ ó õ R  f( x,y) dA

will become when integrated over S in the uv-coordinate system?

36. The bipolar coordinate system on the xy-plane is given by

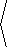
T( u,v) =  sinh( v) cosh(v) -cos( u) ,  sin( u) cosh(v) -cos( u)

If T maps a region S in the uv-plane to a region R in the xy-plane, then what does the change of variable formula imply that

ó õ ó õ R  f( x,y) dA

will become when integrated over S in the uv-coordinate system?

37. Write to Learn: The translation T( u,v) = á u+a,v+b ñ translates a region S in the uv-plane to a region R in the xy-plane which is translated a units horizontally and b units vertically. Write a short essay which uses the change of coordinate formula to show that the area of R is the same as the area of S?

38. Write to Learn: A rotation T( u,v) = á cos( q) u+sin( q)v,-sin( q) u+cos( q) v ñ maps a region S in the uv-plane to a region R in the xy-plane which is rotated about the origin through an angle q. Write a short essay which uses the change of coordinate formula to show that the area of R is the same as the area of S?