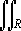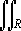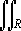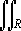Part 2: Centers of Mass

In elementary physics courses, it is shown hat if n objects with masses m₁,m₂,¼,m_n have positions ( x₁,y₁), ( x₂,y₂) ,¼,( x_n,y_n) , respectively, then their center of mass is the point in the plane with coordinates

x  =   m1x1+¼+mnxn m1+¼+mn ,    y  =   m1y1+¼+mnyn m1+¼+mn

If a lamina with mass-density m( x,y) is partitioned into n ``boxes'' with masses Dm<sub>1</sub>,Dm<sub>2</sub>,¼,Dm<sub>n</sub> and positions ( x<sub>1</sub>,y<sub>1</sub>) , ( x<sub>2</sub>,y<sub>2</sub>),¼,( x<sub>n</sub>,y<sub>n</sub>) , respectively, then the center of mass of the lamina is approximately the same as the center of mass of the ``boxes:'' approximately given by

x  »   Dm1x1+¼+Dmnxn Dm1+¼+Dmn ,    y  »  Dm1y1+¼+Dmnyn Dm1+¼+Dmn

However, since Dm₁+¼+Dm_n » M, where M is the mass of the lamina, and since Dm_j » m(x_j,y_j) DA_j, where DA_j is the area of the base of the j^th box, the center of mass of the ``boxes'' can be approximated by

x  »  x1 m( x1, y1) DA1 + ¼ + xn m( xn, yn) DAn M y  »  y1 m( x1, y1) DA1 + ¼ + yn m( xn, yn) DAn M

Since the numerators are approximately the same as double integrals, we are led to define the center of mass of the lamina of a region R to be the point in the xy-plane with coordinates

x  =    1 M 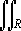x m( x,y) dA,   y  =   1 M  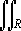y m( x,y) dA

where M is the mass of the lamina.      

EXAMPLE 3    Find the center of mass of the lamina of the unit square with mass density

m( x,y) = ( x+2y )  kg m2

Solution: In example 1, we saw that the mass of the lamina is M = 1.5 kg. Thus,

x =  1 1.5  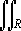xm( x,y) dA =  1 1.5 ó õ 1 0  ó õ 1 0  x( x+2y) dydx =  1 1.5 ó õ 1 0  ( x2+x) dx = 0.5556

Likewise, the y-coordinate of the center of mass is

y =  1 1.5 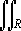ym( x,y) dA =  1 1.5 ó õ 1 0  ó õ 1 0  y( x+2y) dydx = 0.6111

       

When the mass density of the lamina is m( x,y) = 1 for all ( x,y) in the region R, then the center of mass is defined only by the region itself and is thus called the centroid of R. Indeed, the mass M reduces to the area A of the region and thus,

x  =   1 A    xdA,   y  =   1 A ydA

Moreover, if the region is symmetric about a line l, then as we will show in the exercises, the centroid of the region must lie on the line l.       

EXAMPLE 4    Find the centroid of the region R bounded by x = 0, x = 2, y = -x,.y = x

       
Solution: First, we compute the area of the region

A = 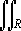dA = ó õ 2 0  ó õ x -x  dydx = 4

As a result, we have

x  =  1 4  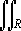xdA  =  1 4 ó õ 2 0  ó õ x -x  xdydx  =  1 4 ó õ 2 0  2x2dx  =  4 3

and since the region R is symmetric about the line y = 0, we must have

y  = 0

LiveGraphics3d Applet