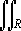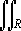Part1: Mass Density

The double integral has many interpretations other than volume. In this section, we examine several of those different interpretations. Many of these intepretations will involve a lamina of a region R in the xy-plane, which is a solid with a constant height whose base is the region R.  Often we simply assume the height is 1.

To begin with, let us suppose that the lamina has a mass-density of m( x,y) , measured in units of mass per unit area (m is the greek letter mu, pronounced ``mew''). In particular, suppose the x and y-axes are both partitioned into h-fine partitions. Then the ``box'' containing the point ( x,y) has a small mass Dm and a small base with area DA, and the mass density function is then defined

m( x,y) = lim h® 0   Dm DA

That is, we define the mass density function so that Dm » m( x,y) DA

As a result, the mass M of the lamina is approximately the sum of the masses Dm_jk of the ``boxes'' in the partition

M = lim h® 0  å j  å k  m( xj,yk) DAjk =  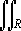 m( x,y) dA

EXAMPLE 1    What is the mass of the lamina of the unit square with a height of 1 and a mass density of

m( x,y) = ( x+2y)     kg m2

Solution: The mass M of the lamina satisfies

M =  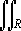( x+2y) dA

where R is the unit square. Thus,

M = ó õ 1 0  ó õ 1 0  ( x+2y) dydx = ó õ 1 0  xy+y2| 01dx = ó õ 1 0  ( x+1) dx = 1.5  kg

       

Notice that if m( x,y) = 1 for all xy in a region, then the mass is simply the product of the height 1 and the area of the base R. As a result, the area A of a region R is given by

A =  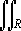dA

EXAMPLE 2    Find the area of the region R bounded by x = 0, x = 1, y = 0 and y = x.       

Solution: The area of the region is given by

A =  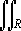 dA =  ó õ 1 0  ó õ x 0  dydx

Evaluating the double integral leads to

A = ó õ 1 0  xdx =  x2 2 ê ê 1 0  =  1 2