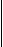Part 2: Volume
If f( x,y) ³ 0 on [ a,b] ×[c,d] , then
f( rj,tk) DxjDyk is the volume of a "box" over a rectangle
determined by partitions of [a,b] and [c,d], respectively.
click on image to change view
Consequently, the Riemann sum is an approximation of the volume of the
solid under z = f( x,y) and over the rectangle [a,b] ×[ c,d] .
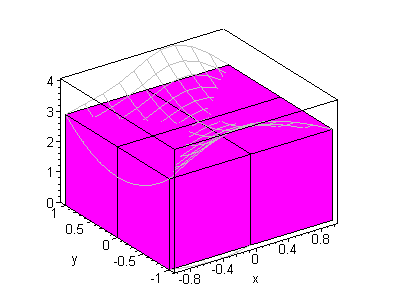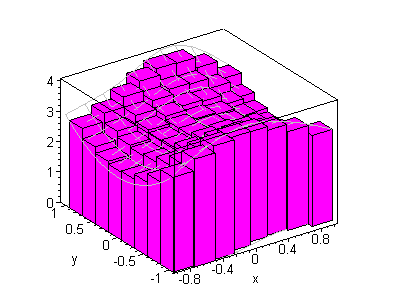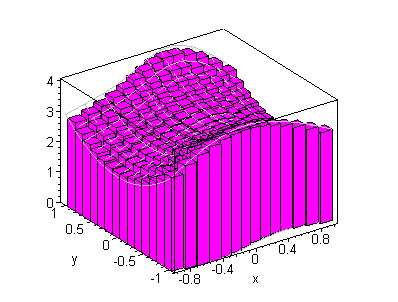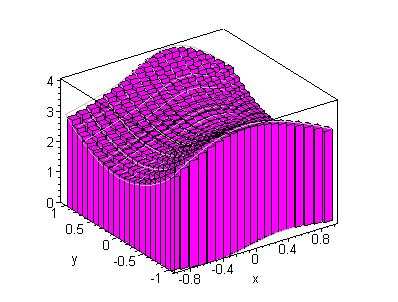
click on image to change view
Thus, if f( x,y) ³ 0
over R,
then the volume of the solid below z = f( x,y) and above R
is
V = 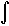 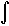 R
f( x,y) dA R
f( x,y) dA |
|
It follows from the previous section that if R is a type I region bounded
by x = a, x = b, y = h( x) , y = g( x) , then
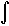 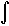 |
R |
f( x,y) dA = |
ó
õ
|
b
a
|
|
ó
õ
|
g(x)
h( x)
|
f( x,y) dydx |
|
and if R is a type II region bounded by y = c, y = d, x = q( y) , x = p( y) , then
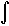 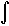 R
f( x,y) dA = R
f( x,y) dA = |
ó
õ
|
d
c
|
|
ó
õ
|
p(y)
q( y)
|
f( x,y) dxdy |
|
EXAMPLE 2 Find the volume of the region below z = x2y and
over the region
Solution: Since the region is a type I region, we obtain
|
|
|
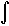 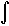 R x2y dA = R x2y dA = |
ó
õ
|
1
0
|
|
ó
õ
|
1
x
|
x2y dydx |
| |
|
| |
|
|
|
ó
õ
|
1
0
|
|
æ
è
|
|
x2
2
|
- |
x4
2
|
ö
ø
|
dx |
| |
|
|
|
In general, if f( x,y) ³ g( x,y) over a
region R,

then the volume of the solid between z = f( x,y) and z = g(x,y) over R is
V = 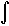 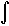 R [ f( x,y) -g( x,y) ] dA R [ f( x,y) -g( x,y) ] dA |
| (5) |
If R is type I or type II, then (5) can be evaluated by
reducing to either a type I or a type II integral, respectively.
EXAMPLE 3 Find the volume of the solid between z = x+y and z = x-y over the region
Solution: According to (5), the volume of the
solid is
V = 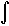 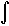 R ( ( x+y) -( x-y) )dA = R ( ( x+y) -( x-y) )dA = 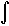 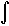 R 2y dA R 2y dA |
|
which transforms into the type II iterated integral
|
V = |
ó
õ
|
1
0
|
|
ó
õ
|
y
y2
|
2y dxdy |
|
Evaluating the inside integral results in
|
V = |
ó
õ
|
1
0
|
2y x |
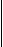 |
|
dy = |
ó
õ
|
1
0
|
( 2y·y-2y·y2) dy |
|
It then follows that
|
V = |
ó
õ
|
1
0
|
( 2y2-2y3) dy = |
1
6
|
|
|
Check your Reading: What type of region is the region R
given in example 3?



R x2y dA =

R ( ( x+y) -( x-y) )dA =
R 2y dA