Part 3: Volumes by Slicing over Type I Regions
Let g, h be continuous on [ a,b] and suppose that g( x) £ h( x) for x in [ a,b] . If R is a region in the xy-plane which is bounded by the curves
y = g(x) to y = h(x) for x
in [a,b] ,
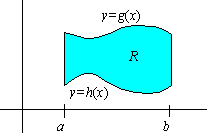
then R is said to be a type I region. Let's find the volume of the
solid between the graph of f( x,y) and the xy-plane over a
type I region R when f( x,y) ³ 0.
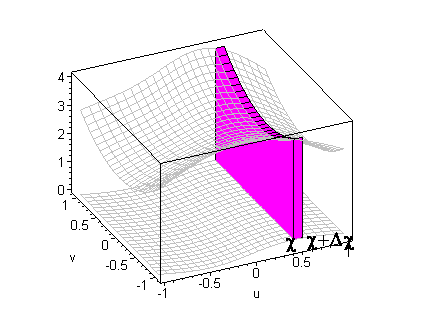
click on image to change view
To do so, let's notice that if the solid is sliced with a plane parallel to
the xz-plane, then its area is
|
A( x) = |
ó
õ
|
h( x)
g( x)
|
f(x,y) dy |
|
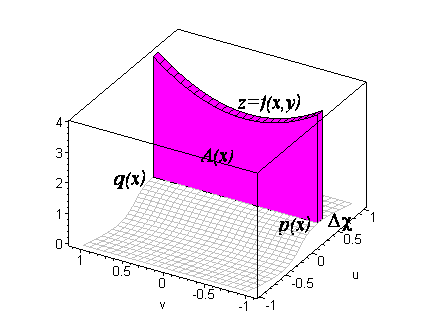
click on image to change view
It follows that if { xj ,tj} , j = 1,¼,n, is a
tagged partition of [ a,b] , then the volume of the solid under
the graph of f( x,y) and over the region R is
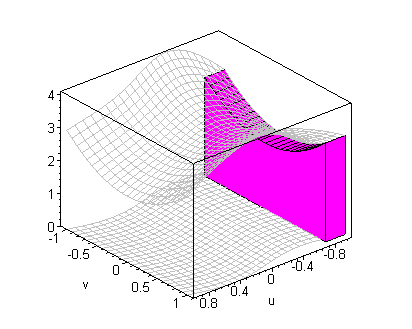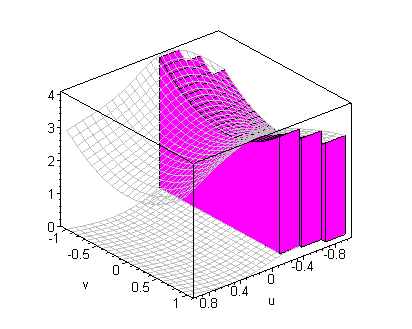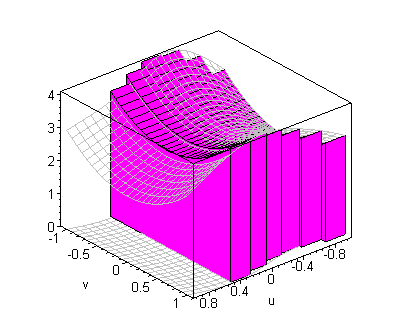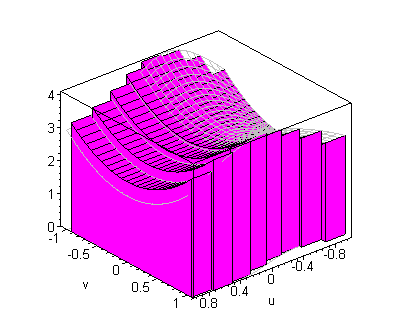
click on image to change view
A limit of such simple function approximations yields the volumes by
slicing formula
which is illustrated below
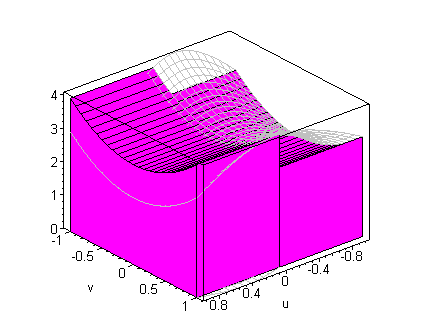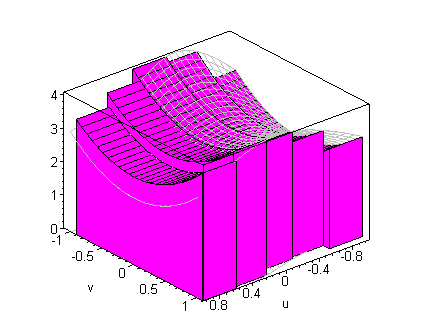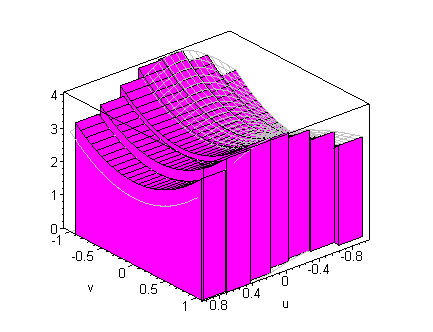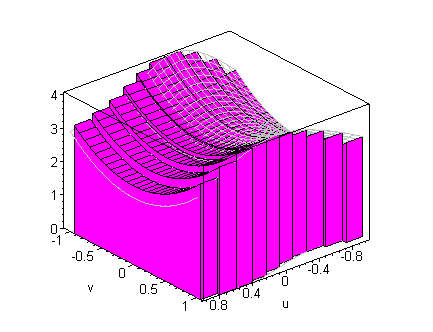
click on image to change view
After combining this with the definition of A( x) , the
result is the iterated integral
|
V = |
ó
õ
|
b
a
|
|
é
ë
|
|
ó
õ
|
h( x)
g( x)
|
f(x,y) dy |
ù
û
|
dx |
| (1) |
EXAMPLE 5 Find the volume of the solid under the graph of f( x,y) =
2-x2-y2 over the type I region
Solution: According to (1), the volume of the solid
is
|
V = |
ó
õ
|
1
0
|
|
é
ë
|
|
ó
õ
|
x
0
|
( 2-x2-y2) dy |
ù
û
|
dx |
|
We evaluate the resulting type I iterated integral by first evaluating the
innermost integral:
|
|
|
|
|
ó
õ
|
1
0
|
|
é
ë
|
2y-x2y- |
y3
3
|
ê
ê
|
x
0
|
ù
û
|
dx |
| |
|
|
|
ó
õ
|
1
0
|
|
é
ë
|
2x- |
4
3
|
x3 |
ù
û
|
dx |
| |
|
|
|
Check your Reading:
Why is 2 - x2 - y2 non-negative over the
region bounded by x = 0, x = 1, y = 0, y = x?





