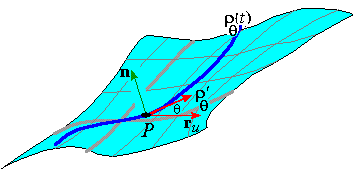
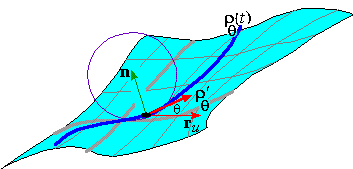
Normal Curvature

If P is a point on an orientable surface S and if r( u,v) is an orthogonal parameterization of a coordinate patch on S containing P, then there is (p,q) such that r( p,q) = P.  Thus, for each q in [ 0,2p] , the curves

rq(t) =  r( p + tcos(q),  q +  tsin(q)  )

pass through P (i.e.,  r_q( 0) = r( p,q) = P ) and the tangent vectors r_q' (0) point in a different direction in the tangent plane to S at P. Indeed, every direction in the tangent plane is parallel to r_q' ( 0) for some q.  

Consequently, the curvatures of r_q( t) at P represent all the different ways that the surface "curves away" from the tangent plane at P.  Correspondingly, we define k_n( q) to be the component of the curvature of r_q( t) at P in the direction of the unit normal

n =  ru×rv ||ru×rv||

In particular, the normal curvature satisfies v² k_n( q)  =  r_q'' (0) · n, so that

kn( q) =  rq'' ( 0) ·  n || rq' (0) ||2

(3)

The unit surface normal n is not necessarily the same as the unit normal N for the curve.  They may point in opposite directions or even be orthogonal - e.g., the normal N to a curve in the xy-plane is in the xy-plane itself yet n = k for the xy-plane.  Thus, the normal curvature k_n(q) is a measure of how much the surface is curving rather than how much the curve is curving. That means that k_n( q) may be positive, negative, or even 0 - e.g., the normal curvature of the xy-plane is 0 even though there are curves in the xy-plane with nonzero curvature.

EXAMPLE 3    Use (3) to find the normal curvature k_n(q) for the cylinder

r( u,v) = á cos( u) ,sin(u) ,v ñ

at the point r( 0,0) = ( 1,0,0) .  

Solution: The curves r_q( t) = r( tcos(q),  tsin( q)) are given by

rq( t) = á cos( tcos( q) ) ,sin( tcos( q)) ,tsin( q) ñ

Differentiation with respect to t leads to

rq' = á -sin( tcos(q) ) cos( q) ,cos( tcos(q) ) cos( q) ,sin( q) ñ rq''   = á -cos( tcos( q) ) cos2( q) ,-sin(tcos( q) ) cos2( q),0 ñ

so that at t = 0 we have

rq' ( 0) = á -sin( 0) cos( q) ,cos( 0) cos(q) ,sin( q) ñ = á0,cos( q) ,sin( q) ñ rq'' ( 0) = á-cos( 0) cos2( q) ,-sin( 0)cos2( q) ,0 ñ = á -cos2( q) ,0,0 ñ

The partial derivatives of r( u,v) are

ru = á -sin( u) ,cos( u),0 ñ ,        rv = á 0,0,1 ñ

which are both unit vectors.  It follows that r_u(0,0) = á 0,1,0 ñ = j and r_v = á 0,1,0 ñ = k.  Thus,

n = ru( 0,0) ×rv(0,0) = j×k = i

Since r_q' ( 0) is a unit vector, we have

kn( q) =  rq'' ( 0) ·n || rq' ( 0) ||2 =   á-cos2( q) ,0,0 ñ ·i 1 = -cos2( q)

That is, if we slice the cylinder along the vector v( q) through a normal to the surface at a point P, then the curvature at P of the curve formed by the intersection is k_n (q) = -cos²(q) .  To illustrate, consider that in the applet below each blue curve is a circle with radius 1/cos²(q).  

LiveGraphics3d Applet The angle is θ = thet °.      The curvature is κ n(θ) = -ax^2

The average of the principal curvatures is called the Mean curvature of the surface and is denoted by H. It can be shown that if C is a sufficiently smooth curve, then the surface with C as its boundary curve that has the smallest possible area must have a mean curvature of H = 0.  For example, consider two parallel circles in 3 dimensional space. 

LiveGraphics3d Applet

The catenoid is the surface connecting the two circles that has the least surface area, and a catenoid also has a mean curvature of H = 0. 

LiveGraphics3d Applet

 

Because they also have the least surface area for their given boundary., surfaces with a mean curvature of H = 0 are called minimal surfaces.  This and other properties mean that minimal surfaces have a large number of applications in architecture, mathematics, and engineering.