Surface Normals and Tangent Planes to Level Surfaces   

Because the equation of a plane requires a point and a normal vector to the plane, finding the equation of a tangent plane to a surface at a given point requires the calculation of a surface normal vector. In this section, we explore the concept of a normal vector to a surface and its use in finding equations of tangent planes.

To begin with, a level surface U( x,y,z) = k is said to be smooth if the gradient ÑU = áU_x,U_y,U_z ñ is continuous and non-zero at each point on the surface. Equivalently, we often write the gradient as

ÑU = Uxex+Uyey+Uzez

where e_x = á 1,0,0 ñ , e_y = á 0,1,0 ñ , and e_z = á0,0,1 ñ .

Suppose that r( t) = á x( t), y(t), z( t) ñ is a curve that lies on a smooth surface U(x,y,z) = k. Applying the derivative with respect to t to both sides of the equation of the level surface yields

dU dt  =    d dt k

Since k is a constant, the chain rule implies that

ÑU · v = 0

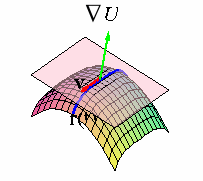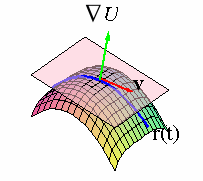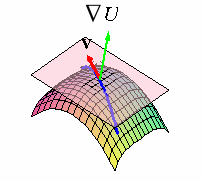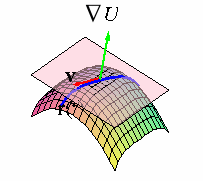
where v = á x' (t), y' (t), z' (t) ñ. However, v is tangent to the surface because it is tangent to a curve on the surface, which implies that ÑU is orthogonal to each tangent vector v at a given point on the surface.

click image to toggle animation

That is, ÑU(p,q,r) at a given point (p,q,r) is normal to the tangent plane to the surface U( x,y,z) = k at the point (p,q,r). We thus say that the gradient ÑU  is normal to the surface U(x,y,z) = k at each point on the surface.

EXAMPLE 1    Find the equation of the tangent plane to the hyperboloid in 2 sheets

x2 - y2 - z2 = 4

at the point ( 3,2,1) .      

Solution: To begin with, we identify U( x,y,z) = x²-y²-z², so that its gradient is

ÑU = á 2x,-2y,-2z ñ

As a result, at the point ( 3,2,1 ) a normal to the tangent plane is given by

n = ÑU( 3,2,1) = á 6,-4,-2 ñ

It follows that the equation of the tangent plane is

6( x-3) -4( y-2) -2( z-1) = 0

which simplifies to the equation z = 3x-2y-4.

Maple/Javaview Figure

EXAMPLE 2    Find the equation of the tangent plane to the right circular cone

x2+y2 = z2

at the point (0.6, 0.8, 1) .       

Solution: Since the equation of the surface can be written x²+y²-z² = 0, we let U( x,y,z) = x²+y²-z². As a result, the gradient of U is

ÑU = á 2x,2y,-2z ñ

At the point ( 0.6, 0.8, 1) , a normal vector is ÑU = á 1.2, 1.6, -2 ñ , so that the equation of the tangent plane is

1.2( x-0.6) +1.6( y-0.8) -2( z-1) = 0

Solving for z then yields z =  0.6x + 0.8y, which is shown in the figure below: