Conic Sections   

A conic section is the curve formed by the intersection of a plane with the right circular cone x²+y² = z². For example, the plane in the conic explorer below is given by z = p+ex, where p is the parameter of the conic and e > 0 is its eccentricity.  If e = 0, then the conic is a circle. If 0 < e < 1, then the conic is an ellipse. If e = 1, then the conic is a parabola, and if e > 1, then the conic is a hyperbola (click here to open applet in a new window).

In cylindrical coordinates, the plane is given by z = p+ercos( q) and the cone is given by r² = z². As a result, the intersection of the plane and the cone is given by

r  =  p + ercos( q) r - ercos(q)  =  p r( 1 - ecos(q) )  =  p

which results in

r =   p 1-ecos( q)

(6)

 

As a result, z = ± r and cylindrical coordinates implies that parameterization of the conic itself is

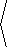
r(q) =  pcos( q) 1-ecos( q) ,  psin(q) 1-ecos( q) ,  p 1-ecos( q)

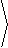where we use the vector-valued funtion r since its length is the spherical coordinate distance r.      

EXAMPLE 7    Find the projection of the conic with eccentricity e = 1 and parameter p = 4. What type of conic is it? What is the parameterization of the conic itself?       

Solution: The projection is given by (6) with e = 1 and p = 4:

r =  4 1-cos( q)

This is a parabola with parameter p = 4. It is parameterized by

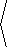
r(q) =  4cos( q) 1-cos( q) ,  4sin( q) 1-cos( q) ,  4 1-cos( q)

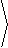which is shown below:

LiveGraphics3d Applet

       

Conic projections of the form (6) are symmetric about the x-axis. Arbitrary conic projections follow from the intersection of the cone with an arbitrary plane, which is given by z = ax+by+p with a,b, and p constant.      

EXAMPLE 8    Find the projection of the conic formed by the intersection of z = 3+0.5y with the right circular cone. What type of conic is it? What is the parameterization of the conic itself?       

Solution: The intersection of z = 3+0.5y with the right circular cone r² = z² is given by

r = 3 + 0.5rsin( q)         Þ        r -  0.5 rsin( q) = 3

which results in the projection

r =   3 1-0.5sin( q)

This is an ellipse with parameter p = 3 and eccentricity e = 0.5 that is symmetric about the y-axis. Moreover, the conic itself has the parameterization

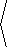
r( q) =  3cos( q) 1-0.5sin( q) ,  3sin( q) 1-0.5sin( q) ,  3 1-0.5sin( q)

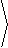which is shown below:

LiveGraphics3d Applet