The Jacobian Determinant   

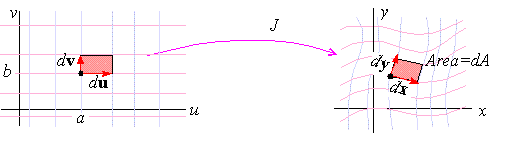
Let T( u,v) be a smooth coordinate transformation with Jacobian J( u,v) , and let R be the rectangle spanned by du = á du,0 ñ and dv = á0,dv ñ . If du and dv are sufficiently close to 0, then T( R) is approximately the same as the parallelogram spanned by

dx = J( u,v) du   and   dy = J(u,v) dv

If we let dA denote the area of the parallelogram spanned by dx and dy, then dA approximates the area of T(R) for du and dv sufficiently close to 0.

Moreover, dA = || dx×dy|| , where dx = áx_udu,y_udu,0 ñ and dy = áx_vdv,y_vdv,0 ñ . An elementary calculation yields

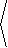
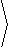
dx×dy = 0,0, ê ê ê xu xv yu yv ê ê ê dudv

from which it follows that

dA = || dx×dy || = | xuyv-xvyu| dudv

(1)

Thus, the area differential dA is given by

dA =   ê ê  ¶( x,y) ¶( u,v) ê ê dudv

That is, the area of a small region in the uv-plane is scaled by the Jacobian determinant to approximate areas of small images in the xy-plane.        

EXAMPLE 5    Find the Jacobian determinant and the area differential of T( u,v) = áu²-v²,2uv ñ at ( u,v) = ( 1,1) , What is the approximate area of the image of the rectangle [1,1.4]×[1,1.2]?        

Solution: The Jacobian determinant is

¶( x,y) ¶( u,v) =  ¶x ¶u  ¶y ¶v  -   ¶x ¶v  ¶y ¶u = ( 2u) ( 2u) -( -2v) ( 2v) = 4u2+4v2

Thus, the area differential is given by

dA =  ê ê  ¶( x,y) ¶( u,v) ê ê dudv = ( 4u2+4v2) dudv

On the rectangle [1,1.4]×[1,1.2], the variable u changes by du = 0.4 and v changes by dv = 0.2. We evaluate the Jacobian at (u,v) = (1,1) and obtain the area

dA = (4·12+4·12)·0.4·0.2 = 0.32

which is the approximate area in the xy-plane of the image of [ 1,1.4] ×[ 1,1.2] under T( u,v) .

Let's look at another interpretation of the area differential.  If the coordinate curves under a transformation T(u,v) are sufficiently close together, then they form a grid of lines that are "practically straight" over short distances.  As a result, sufficiently small rectangles in the uv-plane are mapped to small regions in the xy-plane that are practically the same as parallelograms.

Consequently, the area differential dA approximates the area in the xy-plane of the image of a rectangle in the uv-plane as long as the rectangle in the uv-plane is sufficiently small.                

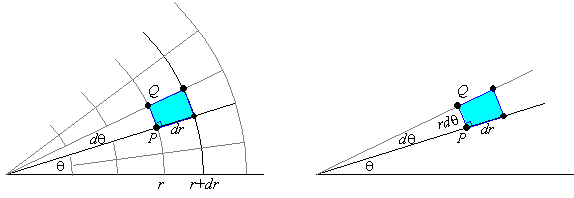
EXAMPLE 6    Find the Jacobian determinant and the area differential for the polar coordinate transformation. Illustrate using the image of a "grid" of rectangles in polar coordinates.

Solution: Since x = rcos( q) and y = rsin( q) , the Jacobian determinant is

¶( x,y) ¶( r,q) =  ¶x ¶r  ¶y ¶q -  ¶x ¶q  ¶y ¶r = cos( q) rcos( q) -rsin(q) sin( q) = r[ cos2( q) +sin2( q) ] = r

Thus, the area differential is dA = rdrdq.
    Geometrically, "rectangles" in polar coordinates are regions between circular arcs and rays through the origin.  If the distance changes from r to r+dr when r > 0 for some small dr > 0, and if the polar angle changes from q to q+dq for some small angle dq, then the region covered is practically the same as a small rectangle with height dr and width ds, which is the distance from q to q+dq along a circle of radius r.
If an arc subtends an angle dq of a circle of radius r, then the length of the arc is ds = rdq. Thus,

dA = dr ds = rdrdq