Exercises

Find the Jacobian determinant and area differential of each of the following transformations.

7. T( u,v) = á u+v,u-v ñ 8. T( u,v) = á uv,u-v ñ 9. T( u,v) = á u2-v2,2uv ñ 10. T( u,v) = áu3-3uv2,3u2v-v3 ñ 11. T( u,v) = á uev,ue-v ñ 12. T( u,v) = á eucos( v) ,eusin( v) ñ 13. T( u,v) = á 2ucos( v) ,3usin( v) ñ 14. T( u,v) = áu2cos( v) ,u2sin( v) ñ 15. T( u,v) = á eucos( v),e-usin( v) ñ 16. T( u,v) = á eucosh( v) ,e-usinh( v) ñ 17. T( u,v) = á sin( u) sinh(v) ,cos( u) cosh( v) ñ 18. T( u,v) = á sin( uv) ,cos(uv) ñ

In each of the following, sketch several coordinate curves of the given coordinate system to form a grid of "rectangles" (i.e., make sure the u-curves are close enough to appear straight between the v-curves and vice-versa.  Find the area differential and discuss its relationship to the "coordinate curve grid". (19 - 22 are linear transformations and have a constant Jacobian determinant)

19. T( u,v) = á 2u,v ñ 20. T( u,v) = á u+1,v ñ 21. T( u,v) =  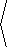u-v Ö2 ,  u+v Ö2 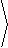22. T( u,v) =  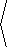u-Ö3v 2 ,  Ö3u+v 2   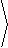        23. parabolic coordinates 22. tangent coordinates T( u,v) = á u2-v2,2uv ñ T( u,v) =  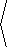u u2+v2 ,  v u2+v2   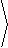        25. elliptic coordinates 24. bipolar coordinates T( u,v) = á cosh( u) cos(v) ,sinh( u) sin( v) ñ T( u,v) =  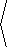sinh( v) cosh(v) -cos( u) ,  sin( u) cosh(v) -cos( u)

  

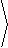 Some of the exercises below refer to the following formula for the inverse of the Jacobian:

J-1( x,y)  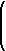=    ¶( x,y) ¶( u,v)  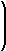-1   é ê ë   yv -xv -yu xu ù ú û

(4)

27.  Find T^-1( x,y) for the transformation

T( u,v) = á u+v, u-v ñ

by letting x = u+v, y = u-v and solving for u and v.  Then find J^-1(x,y) both (a) directly from T^-1( x,y) and (b) from the formula (4).

28.  Find T^-1( x,y) for the transformation

T( u,v) = á u+4, u-v ñ

Then find J^-1( x,y) both (a) directly from T^-1(x,y) and (b) from the formula (4).        

29. At what points ( u,v) does the coordinate transformation

T( u,v) = á eu cos(v),  eu sin(v) ñ

have an inverse? What is the inverse T^-1(x,y)?  What is its Jacobian?

30. At what points ( u,v) does the coordinate transformation

T( u,v) = á ucosh(v), usinh(v) ñ

have an inverse. What is the inverse T^-1(x,y)?  What is its Jacobian?

31. Show that if T( u,v) = áau+bv, cu+dv ñ where a,b,c,d are constants (i.e., T(u,v) is a linear transformation ), then J( u,v) is the matrix of the linear transformation T( u,v) .

32. Show that if T( u,v) = áau+bv, cu+dv ñ where a,b,c,d are constants (i.e., T(u,v) is a linear transformation ), then

¶( x,y) ¶( u,v) = ad - bc

33. Show that if f( u,v) is differentiable, then

¶( f, f) ¶( u, v) = 0

34. Show that if f( u,v) and g( u,v) are differentiable and if k is constant, then

¶( kf,g) ¶( u, v) = k  ¶( f, g) ¶( u, v)

35.  Explain why if x > 0, then the inverse of the polar coordinate transformation is

T-1( x,y) =  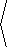  x2+y2 ,  tan-1 æ è    y x ö ø

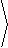36. The Jacobian Matrix of ( r,q) = T^-1(x,y) is

K( x,y) = é ê ë   rx ry qx qy ù ú û

Find K( x,y) for T^-1( x,y) in exercise 35, and then use polar coordinates to explain its relationship to

J-1( r,q) =  1 r   é ê ë   rcos( q) rsin( q) -sin( q) cos( q) ù ú û

37. Show that if x < 0, then the inverse of the polar coordinate transformation is

T-1( x,y) =  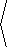  x2+y2 ,  p + tan-1 æ è    y x ö ø

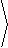38. Use the following steps to show that if ( x,y) is not at the origin or on the negative real axis, then

T-1( x,y) = x2+y2 , 2tan-1 æ ç è    y x+ x2+y2 ö ÷ ø

is the inverse of the polar coordinate transformation. 

       a. Verify the identity

tan( f) =  sin( 2f) 1+cos(2f)

       b. Let f = q/2 in a. Multiply numerator and denominator by r.

       c. Simplify to an equation in x, y, and q.

39. The coordinate transformation of rotation about the origin is given by

T( u,v) = á cos(q) u + sin(q) v,  -sin(q) v + cos(q)u ñ

where q is the angle of rotation. What is the Jacobian determinant and area differential for rotation through an angle q? Explain the result geometrically.

40. The coordinate transformation of scaling horizontally by a > 0 and scaling vertically by b > 0 is given by

T( u,v) = á au, bv ñ

What is its area differential? Explain the result geometrically.

41. A transformation T(u, v) is said to be a conformal transformation if its Jacobian matrix preserves angles between tangent vectors. Consider that the vector á0, 1 ñ is parallel to the line r = p and that the vector á 1,1 ñ is parallel to the line r = q. Also, notice that r = p and r = q intersect at ( r,q) = ( p,p) at a 45^° angle.
For J( r,q) for polar coordinates, calculate

v = J( p,p) é ê ë   0 1 ù ú û   and  w = J( p,p) é ê ë   1 1 ù ú û

Is the angle between v and w a 45^° angle? Is the polar coordinate transformation conformal?

42. Find the Jacobian and repeat exercise 41 for the transformation

T( r,q) = á er cos(q), er sin(q) ñ

43. Write to Learn: Write a short essay in which you calculate the area differential of the transformation T( r,q) = á e^rcos( q) ,e^rsin(q) ñ both computationally and geometrically.

44. Write to Learn: A coordinate transformation T( u,v) = á f( u,v) ,g( u,) ñ is said to be area preserving if the area of the image of any region R in the uv-plane is the same as the area of R. Write a short essay which uses the area differential to explain why a rotation through an angle q is area preserving.

45. Proof of a Simplified Inverse Function Theorem: Suppose that the Jacobian determinant of T( u,v) = á f(u,v), g(u,v) ñ is non-zero at a point ( p,q) and suppose that r( t) = á p+mt, q+nt ñ, t in [ -e,e] , is a line segment in the uv-plane (m and n are numbers). Explain why if e is sufficiently close to 0, then there is a 1-1 correspondence between the segment r( t) and its image T( r( t) ) , t in [-e,e] . (Hint: first show that x(t) = f( p+mt, q+nt) is monotone in t for t in [-e,e] ).

46. Write to Learn: Let T( u,v) = áx( u,v) ,y( u,v) ñ be differentiable at p = ( p,q) and assume that its Jacobian matrix is of the form

J = é ê ë   a b c d ù ú û

By letting u = á p+h, q ñ in definition 3.1, (so that u-p = [ h  0] ^t in matrix notation ), show that

lim u® p     | T( u) - T( p)  -  J( p) ( u-p) | || u-p || = 0

is transformed into

lim h® 0+     || á x(p+h,q) -x( p,q),  y( p+h,q) - y( p,q) ñ - á ah, ch ñ | | h = 0

Use this to show that a = x_u and c = y_u. How would you find b and d? Explain your derivations and results in a short essay.