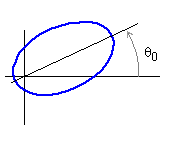Ellipses in Polar Coordinates

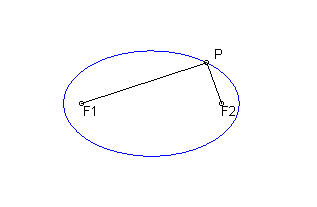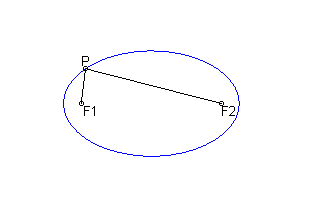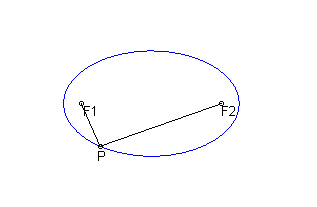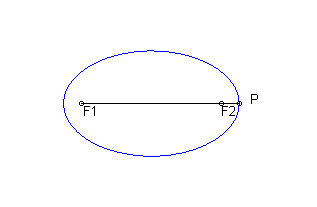
Let's suppose that 2 ''nails'' are driven into a board at points F₁ and F₂, and suppose that the ends of a string of length 2a is attached to the board at points F₁ and F₂. If the string is pulled tight around a pencil's tip, then the points P traced by the pencil as it moves within the string form an ellipse.

click image to toggle animation

Let's use this definition of an ellipse to derive its representation in polar coordinates. To begin with, let's assume that F₁ is at the origin and that F₂ is on the positive real axis. Then the distance |PF₁| is the same as the r in polar coordinates

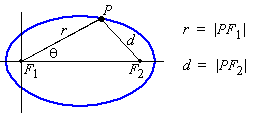
Let's use this definition of an ellipse to derive its representation in polar coordinates. To begin with, let's assume that F₁ is at the origin and that F₂ is on the positive real axis at the point (2c,0) (i.e., 2c is the distance from F₁ to F₂). Then r is the polar vector to the point P, and r-2ci  is the vector from F₂ to P.   The ellipse definition implies that

||r||  +  ||r-2ci||   =   2a

Thus, r = ||r|| implies that r-2a = ||r-2ci||, so that

( r-2a) 2  =  ||r-2ci||2

However, r = á rcos( q) ,rsin(q) ñ implies that

( r - 2a)2 = ( rcosq-2c)2  + ( r sinq)2 ( r - 2a)2 = r2cos2( q) - 2rccos( q) +  4c2 + r2sin2( q) r2 - 4ar + 4a2 = r2 - 4rccos( q) + 4c2

Simplifying and solving for r yields

-4ar + 4a2 = -4rc cos( q) +4c2 -ar + rccos( q) = -a2 + c2 r( -a + ccos( q) ) = -a2 + c2 r =  -a2 + c2 -a + ccos( q)

If we let b² = a²-c² denote the square of the semi-minor axis, then

r =  b2 a - c cos( q)

Finally, let us divide by a to obtain

r =  b2/a 1-c/a cos( q)

Usually, we let e = c/a and let p = b²/a, where e is called the eccentricity of the ellipse and p is called the parameter. It follows that 0 £ e < 1 and p > 0, so that an ellipse in polar coordinates with one focus at the origin and the other on the positive x-axis is given by

r =  p 1-ecos( q)

Moreover, b² = a²-c² implies that

p = a æ è  b2 a2 ö ø = a æ è  a2-c2 a2 ö ø = a æ è 1-  c2 a2 ö ø ,

which in turn implies that p = a( 1-e²) .

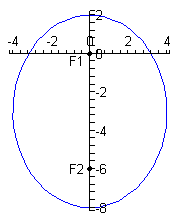
EXAMPLE 7    Find the center, semi-major axis, semi-minor axis and foci of the ellipse

r =  3 1-0.5cos( q)

What is the Cartesian equation of the ellipse?

Solution: Since p = 3 and e = 0.5, the formula p = a( 1-e² ) implies that

a =  3 1-( 0.5) 2 = 4

As a result, b² = ap implies that

b2 = 4·3 = 12,        b = Ö12 = 2Ö3

Finally, the focus F₁ is at the origin and the calculation

2ea = 2·0.5·4 = 4

implies that F₂ is at the point ( 4,0) on the x-axis. To convert to x and y, we first multiply to get

5r  -  4r cos(q) = 9

Thus, 5r = 4rcos( q) +9, so that

25r2 = ( 4rcos(q)  + 9)2 25( x2+y2) = ( 4x + 9)2

Since ( 4x+9) ² = 16x²+72x+81, we have

25x2+25y2 = 16x2+72x+81

which yields 9x²-72x+25y² = 81.  

               

Finally, had F₂ been placed on the positive y-axis, the negative x-axis, or the negative y-axis, the polar equation of the ellipse would be modified by replacing cos( q) with sin( q) , -cos( q) , or -sin( q) , respectively.

Polar ellipses with F2 on the given axis and  F1 = (0,0) positive x-axis:   r =  p 1-ecos( q)                  positive y-axis:   r =  p 1-esin( q) negative x-axis:   r =  p 1+ecos( q)   negative y-axis:   r =  p 1+esin( q)

Indeed, the most general form of an conic with parameter p and eccentricity e > 0 is

r =  p 1-ecos( q-q0)

(3)

where it can be shown that a = ecos( q₀) and b = esin( q₀) . It follows that the conic is symmetric about the line at angle q₀ to the x-axis.

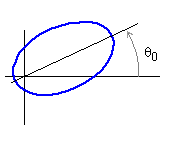
EXAMPLE 8    Find the center, semi-major axis, semi-minor axis and foci of the ellipse

r = 16 5 + 3cos( q)

Solution: Let's divide the numerator and denominator by 5 to obtain

r = 16/5 1 + 3/5 cos( q)

Since p = 16/5 and e = 3/5, the formula p = a( 1-e² ) implies that

a =  16/5 1-( 3/5) 2   =  5

As a result, b² = ap implies that

b2 = 5 ·  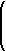 16 5  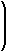 = 16,        b = 4

Finally, the focus F₁ is at the origin and the table above implies that F₂ is on the negative y-axis. Since

2ea = 2· (3/5) · 5 = 6

implies that F₂ is at the point ( 0, -6).