Polar Coordinates in Vector Form   

The fact that x = r cos(q) and y = r sin(q) implies that the graph of r = f( q) is parameterized by

r(q) =  f(q) á cos(q), sin(q) ñ

Thus, tangent vectors, curvature, normals, arclength, etcetera, for polar curves r = f(q) can be obtained by applying techniques and concepts in chapter 1 to r(q) .  

EXAMPLE 6    Find the pullback of x = 1 into polar coordinates. What is the velocity v for the pullback? What is significant about the result.    

Solution: To do so, we let x = rcos( q) , which corresponds to

rcos( q) = 1  or r = sec( q)

Thus, r( q) = sec( q) á cosq, sinq ñ = á 1, tan( q) ñ since secq = 1/cosq  and tan( q) = sin( q) sec(q) .  Consequently,

v =  d dq r =  d dq á1,tan( q) ñ = á 0,sec2(q) ñ

Equivalently, v = sec²(q) á0,1 ñ = sec²( q) j.  That is, the direction is constant (i.e., along the line x = 1 ), but the speed is not ( v = sec²( q) ).

If we let e_r = á cos( q),sin( q) ñ , then the parameterization of a polar curve is given by

r(q) =  r(q)  er

It follows that the velocity of r(q) is

v( q) = é ë  d dq r( q) ù û   á cos( q) ,sin(q) ñ +r( q)  d dq á cos( q) ,sin( q) ñ = r' (q)  er   +   r(q)  á -sin(q), cos(q) ñ (1)

If we let e_q = á -sin(q), cos(q) ñ,  then (1) becomes

v( q) = r' er+r eq

The vectors e_r and e_q are unit vectors that satisfy e_r · e_q = 0.  Thus, for each value of q, the vectors e_r and e_q form an orthonormal basis in polar coordinates, much like the vectors i = e_x and j = e_y do in Cartesian coordinates. However, as we move from point-to-point in the plane, the e_r and e_q vectors change direction whereas the e_x and e_y vectors do not.

LiveGraphics3d Applet Drag the red dots. The er and eq have different  directions at different points, but ex and ey have fixed directions.

This reflects the fact that Cartesian coordinates are formed by 2 families of parallel lines, while polar coordinates are not.

EXAMPLE 7    Sketch the graph of r = 2sin( 3q) .  What is the slope of the tangent line to the curve at q = p/6?

Solution: When q = 0 or q = p/3, then r = 2sin( 0) = 2sin( p) = 0. Thus, the graph of r = 2sin( 3q) forms a single loop for q in [ 0,p/3] . It then follows that it forms another loop when q is in [ p/3,2p/3] and yet another loop for q in [2p/3,p] .
Substituting r = 2sin( 3q) into the parameterization yields

r( q) = 2sin( 3q) er

which has a derivative of

v(q) =  d dq ( 2 sin(3q) er) = 6cos(3q) er  +  2sin(3q) eq

since de_r/dq = e_q.  Thus, at q = p/6 we have

v æ è  p 6 ö ø = 6cos æ è  p 2 ö ø er+2sin æ è  p 2 ö ø eq = 0+2eq

Evaluating e_q = á -sinq,cosq ñ at q = p/6  leads to

eq =  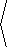-1 2 ,  Ö3 2

so that p>

v æ è  p 6 ö ø = 2  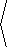-1 2 ,  Ö3 2 = á -1,Ö3 ñ

Thus, the tangent line has a slope of m = -Ö3.

Alternatively, in example 7, we could have used the expanded form

r( q) = 2sin( 3q)   ácosq, sinq ñ

when determining v.  The basis notation e_r, e_q is simply a more compact method for doing same thing.  

    Check Your Reading: How did we obtain m = -Ö3 from the velocity vector in example 7?