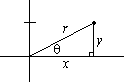The Polar Coordinate Transformation

If we choose the ray l to be the positive x-axis, then a point  P in the plane has both cartesian coordinates ( x,y) and polar coordinates (r, q).

(2)

The definition of the sine and cosine functions imply that (x,y) is given in terms of ( r,q) by

x = r cos(q) ,        y = r sin(q)

(1)

Solving for r and q then yields the identities

r2 = x2+y2    and     tan( q) =  y x

(2)

EXAMPLE 3    Convert the point ( 4, p/4) from polar coordinates into cartesian coordinates, and then show that (2) converts it back into polar .       

Solution: To do so, we let r = 4 and let q = p/4 in (1) to obtain

x = 4cos æ è p 4 ö ø = 2Ö2,        y = 4sin æ è p 4 ö ø = 2Ö2

To map back, we notice that

r2   =  x2 + y2 = 8 + 8 = 16,  r = 4

and that y/x = 1 implies that tan(q) = 1, q = p/4.

If we substitute x = r cos(q) and y = r sin(q) into a curve g(x,y) = k, then the result

g( rcos(q),  rsin(q) ) = k

 is called the pullback of the curve into polar coordinates.  The identity r² = x²+y²  is often used in pulling a curve back into polar coordinates.

For example, x²+y² = R² for a constant R > 0 has a pullback of

r2 = R2   Þ    r = R

Similarly, lines of the form y = mx become

r sin(q) = m r cos(q)    Þ     sin(q) = m cos(q)     Þ     tan(q) = m

This matches example 4 in the last section, in which we saw that the coordinate curves for the polar coordinate transformation

T( r, q ) = á r cos(q),  r sin(q) ñ

 are circles centered at the origin and lines through the origin, respectively.   Also, it shows that whenever possible, we should solve for r to obtain a function of the form r = f(q) .

EXAMPLE 4    Convert the curve x² + (y - 1)² =  1 into polar coordinates, and then solve for r, if possible.       

Solution: Expanding leads to x² + y² - 2y + 1 = 1 , so that To do so, we replace y r² and let x = rcos( q) :

r2 -  2r sin(q) + 1 = 1

Solving for r then yields

r = 2 sin(q)

That is, r = 2 sin(q)  is a circle of radius 1 centered at ( 1,0) . In general, a curve of the form r = 2acos( q) is a circle of radius | a| centered at ( a,0) and a curve of the form r = 2asin(q) is a circle of radius | a| centered at (0, a) .