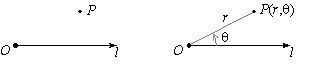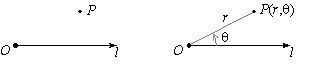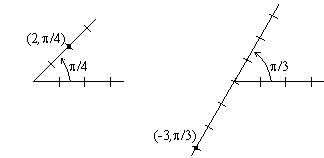Polar Coordinates

Although we introduced  polar coordinates in the previous section, this coordinate transformation occurs frequently enough to warrant our considering it separately.  Let's begin by reviewing what it means to assign polar coordinates to a point the in the plane.

Suppose that l is a ray that begins at an origin O, and suppose that P is a point in the plane. Then P can be located with respect to l and O by specifying both the distance r from O to P and an angle q  formed by the segment OP and the ray l.

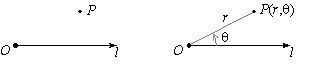
The order pair ( r, q)  is called the polar coordinates of the point P.  

The polar coordinates of a point are not unique.  Since angles repeat every 2p radians, it follows that ( r,q) = ( r,q+2p) . Moreover, a negative value of r implies a rotation of 180^°, so that we also have ( -r,q) = ( r,q+p) .       

EXAMPLE 1    Locate the points ( 2,p/4) and ( -3,p/3) using polar coordinates.       

Solution: The point with polar coordinates ( 2,p/4) must be a distance of 2 from the origin along the ray which is at an angle of p/4 from the x-axis. Likewise, the point with polar coordinates ( -3,p/3) is the same as the point ( 3,p+p/3) , as is shown below:

       

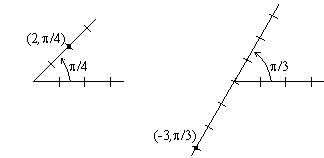
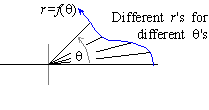
It is customary in polar coordinates to write the distance r as a function of q. In particular, r = f( q) assigns a distance from the origin to each angle q, thus forming a curve.

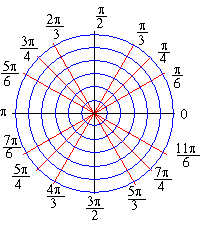
We can produce a rough sketch of a curve in polar coordinates by determining r at key angles, such as q = 0, p/6, p/4, p/3, p/2, 2p/3, etc., and  then plotting those points on a polar coordinate grid such as the one shown below:

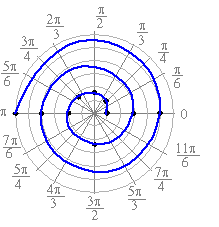
EXAMPLE 4    Sketch the graph of the function

r =  1 p q+1

Solution: First, let us choose some typical values of q and compute r for those angles.

q 0  p 4  p 2  3p 4 p  3p 2 2p 3p 4p r 1 1.25 1.5 1.75 2 2.5 3 4 5

Now let's plot those points on the grid and connect them to obtain a sketch of the graph of the function:

       

  Check your Reading: What type of curve is shown in example 2?