Exercises:

Find the image in the xy-plane of the given curve in the uv-plane under the given transformation. If the transformation is linear, identify it as such and write it in matrix form.

1. T( u,v) = á u, v2 ñ , v = 2u 2. T( u,v) = á uv,u+v ñ , v = 3 3. T( u,v) = á u-2v, 2u+v ñ , v = 0 4. T( u,v) = á u+3,v+2 ñ , u2+v2 = 1 5. T( u,v) = á 4u, 3v ñ , u2+v2 = 1 6. T( u,v) = á u2+v,u2-v ñ , v = u 7. T( u,v) = á u2 - v2,  uv ñ , v = 2 8. T( u,v) = á u2-v2,2uv ñ , u = -1 9. T( r,q) = á rcos(q), rsin( q) ñ ,  r = 1 10. T(r,q) = á rcos( q) ,rsin(q) ñ ,  q = p/4

Find the coordinate curves of the given transformation. Then find the image of the unit square in the uv-plane under the given transformation. If the transformation is linear, identify it as such and write it in matrix form.

11. T( u,v) = á u+1,v+5 ñ 12. T( u,v) = á 2u+1,3v-2 ñ 13. T( u,v) = á v,u ñ 14. T( u,v) = á u+v+1,v+2 ñ 15. T( u,v) = á u2-v2, u + v ñ 16. T( u,v) = á u2+v,u2-v ñ 17. T( u,v) = á 2u+3v,-3u+2v ñ 18. T( u,v) = á ucos( pv) ,usin(pv) ñ 19. Rotation about the origin 20. Rotation about the origin through an angle q =   p 4 through an angle q =   2p 3 21. T( u,v) = á uev,ue-v ñ 22. T( u,v) = á u + v, u + v ñ 23. T( r,q) = á rcos( q),r2sin2( q) ñ 24. T(r,t) = á rcosh( t) ,rsinh( t) ñ

Find a conic in standard form that is the pullback under rotation of the given curve. 

25. 5x2 + 6xy + 5y2 = 8 26. 5x2 - 6xy  + 5y2 = 9 27. xy = 1 28. xy = 4 29. 7x2 + 6Ö3 xy + 13y2 = 16 30. 13x2 - 6Ö3 xy + 7y2 = 16 31. 52x2 - 72xy + 73y2 = 100   32. 73x2 + 72xy + 52y2 = 100

33. The conic section

x2 + 2xy + y2 - x + y = 2

is not centered at the origin.  Can you rotate it into standard position?

34. The conic section

5 x2 + 6xy + 5y2 - 4x + 4y = -2

is not centered at the origin.  Can you rotate it into standard position?

35. Show that if

é ê ë x y ù ú û = é ê ë cos( q) -sin( q) sin( q) cos( q) ù ú û é ê ë u v ù ú û

then we must also have

é ê ë u v ù ú û = é ê ë cos( q) sin( q) -sin( q) cos( q) ù ú û é ê ë x y ù ú û

What is the significance of this result?

36. Use matrix multiplication to show that a rotation through an angle q followed by a rotation through an angle f is equivalent to a single rotation through the angle q+f.

37. The parabolic coordinate system on the xy-plane is the image of the coordinate transformation

T( u,v) = á u2-v2,2uv ñ

Find the image of the horizontal lines u = 0,1,2 and the vertical lines v = 0,1,2 in the parabolic coordinate system.

38. The tangent coordinate system on the xy-plane is the image of the coordinate transformation

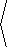
T( u,v) =  u u2+v2 ,   v u2+v2

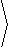Find the image of the horizontal lines u = 0,1,2 and the vertical lines v = 0,1,2 in the tangent coordinate system.

39. The elliptic coordinate system on the xy-plane is the image of the coordinate transformation

T( u,v) = á cosh( u) cos( v),  sinh( u) sin( v) ñ

Find the image of the horizontal lines u = 0,1,2 and the vertical lines v = 0,1,2 in the elliptic coordinate system.

40. The bipolar coordinate system on the xy-plane is the image of the coordinate transformation

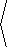
T( u,v) =  sinh( v) cosh(v) -cos( u) ,  sin( u) cosh(v) -cos( u)

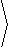Find the image of the horizontal lines u = 0,1,2 and the vertical lines v = 0,1,2 in the bipolar coordinate system.

41. Write to Learn: A coordinate transformation T( u,v) = á f( u,v), g( u,v) ñ is said to be area preserving if the area of the image of any region S in the uv-plane is the same as the area of R. Write a short essay explaining why a rotation through an angle q is area preserving.

42. Write to Learn (Maple): A coordinate transformation T(u,v) = á f( u, v),  g( u, v) ñ is said to be conformal (or angle-preserving) if the angle between 2 lines in the uv-plane is mapped to the same angle between the image lines in the xy-plane. Write a short essay explaining why a linear transformation with a matrix of

A  =    é ê ë a -b b a ù ú û

is a conformal transformation.

43. Write to Learn: What type of coordinate system is implied by the coordinate transformation T( u,v) = á u, F(u) + v ñ?  What are the coordinate curves?  What is significant about tangent lines to these curves?  Write a short essay which addresses these questions.  

44.  Write to Learn:  Suppose that we are working in an XY-coordinate system that is centered at ( p,q) and is at an angle q to the x-axis in an xy-coordinate system.  
Write a short essay explaining how one would convert coordinates with respect to the XY axes to coordinates in the xy-coordinate system.